【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

参考答案:
【答案】(1)四边形EBGD是菱形,理由见解析;(2)![]() .
.
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
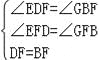 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.
(1)求证:DF=BE;
(2)若
 ,BE=2,求BC的长.
,BE=2,求BC的长.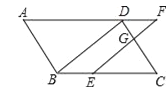
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用乘法公式简便计算:
(1)9982; (2)197×203.
-
科目: 来源: 题型:
查看答案和解析>>【题目】临沂市去年全年的旅游总收入约300.6亿元,将300.6亿元用科学记数法可表示为( )
A.30.06×108元
B.30.06×109
C.3.006×1010元
D.3.006×109元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABO中,AB⊥OB,OB=
 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
A.(-1,-
 )
) B.(-1,-
 )或(-2,0)
)或(-2,0) C.(-
 ,1)或(0,﹣2)
,1)或(0,﹣2) D.(-
 ,1)
,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】有八个球编号是①至⑧,其中有六个球一样重,另外两个球都轻1克,为了找出这两个轻球,用天平称了三次,结果如下:第一次①+②比③+④重,第二次⑤+⑥比⑦+⑧轻,第三次①+③+⑤和②+④+⑧一样重.那么,两个轻球的编号是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )

A. ①②③ B. ①③④ C. ①②③⑤ D. ①③⑤
相关试题

