【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:

表2:四个家庭2017年的年用水量和缴纳水费情况:
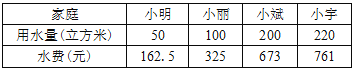
请你根据表1、表2提供的数据回答下列问题:
(1)表1中的![]() __________,
__________,![]() _____________;
_____________;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?
参考答案:
【答案】(1)3.25,180;(2)235立方米.
【解析】
(1)根据小明、小丽、小斌家的年用水量和缴纳水费情况可知100<m<200,从而求出a及m的值;
(2)由年用水量为240立方米时,共缴纳水费849元,而673<827<849,可得她家2017年的年用水量在第二阶梯.设她家2017年的年用水量是x立方米,根据共缴纳水费827元列出方程,求解即可.
(1)由题意,可得:a![]() 3.25,根据小斌家用水200立方米(在第二阶梯),缴纳水费673元,列出方程:3.25m+4.4(200﹣m)=673,解得:m=180.
3.25,根据小斌家用水200立方米(在第二阶梯),缴纳水费673元,列出方程:3.25m+4.4(200﹣m)=673,解得:m=180.
故答案为:3.25,180;
(2)由年用水量为240立方米时,共缴纳水费:3.25×180+4.4(240﹣180)=849(元).
∵673<827<849,∴她家2017年的年用水量在第二阶梯.
设她家2017年的年用水量是x立方米,根据题意,得:
3.25×180+4.4(x﹣180)=827
解得:x=235.
答:她家2017年的年用水量是235立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
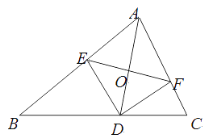
A. ②③ B. ②④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在CB上的A′处,折痕CD,则∠A′DB= ( )
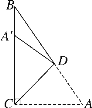
A. 10° B. 20° C. 30° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2
 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动_____个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,运动t秒钟过后:
①点A、B、C表示的数分别是_____、_____、_____ (用含t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2.试问:d1﹣d2的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出d1﹣d2值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位
 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降). 星期
一
二
三
四
五
六
水位
变化(米)
+0.2

-0.4

+0.3
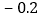
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,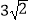
B.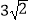 ,3
,3
C.6,3
D.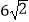 ,
, 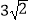
相关试题

