【题目】已知线段AB=42,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE= ![]() AC,求线段DE的长.
AC,求线段DE的长.![]()
参考答案:
【答案】解:∵线段AB=42,点C为AB中点,
∴AC=BC= ![]() AB=
AB= ![]() ×42=21,
×42=21,
∵点D为BC中点,
∴CD=BD= ![]() BC=
BC= ![]() ×21=10.5,
×21=10.5,
∵CE= ![]() AC,
AC,
∴CE= ![]() ×21=7,
×21=7,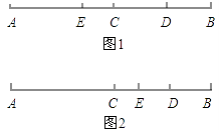
如图1,DE=CD+CE=10.5+7=17.5;
如图2,DE=CD﹣CE=10.5﹣7=3.5.
综上所述,线段DE的长是17.5或3.5.
【解析】根据点C是线段AB的中点,点D是线段CB的中点,可求AC、BC,CD、BD,再由已知条件CE= ![]() AC,可求CE,根据DE=CD+CE或DE=CD﹣CE
AC,可求CE,根据DE=CD+CE或DE=CD﹣CE
线段DE的长可求。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若
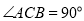 ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF; (3)求出矩形DEFG的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)先化简,再求值:x2+2x﹣3(x2﹣ x),其中x=﹣
x),其中x=﹣  .
.
(2)计算: xy﹣2(xy﹣
xy﹣2(xy﹣  xy2)+(
xy2)+(  xy+
xy+  xy2),其中x、y满足|x﹣6|+(y+2)2=0.
xy2),其中x、y满足|x﹣6|+(y+2)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】在课间活动中,小英、小丽和小敏在操场上画出A,B两个区域,一起玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.
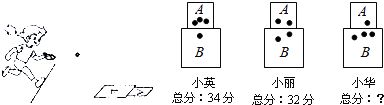
(1)沙包落在A区域和B区域所得分值分别是多少?
(2)求出小敏的四次总分. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位,那么得到的抛物线的表达式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
相关试题

