【题目】如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足 ![]() +(b2﹣16)2=0.
+(b2﹣16)2=0. 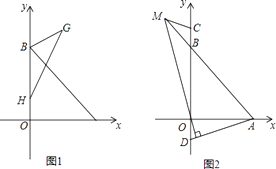
(1)求A、B两点的坐标,∠OAB的度数;
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,
①求点E到BH的距离;
②求点G的坐标;
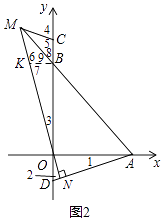
(3)如图2,C,D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
参考答案:
【答案】
(1)解:∵ ![]() +(b2﹣16)2=0,
+(b2﹣16)2=0,
∴a﹣b=0,b2﹣16=0,
解得:b=4,a=4或b=﹣4,a=﹣4,
∵A点在x轴正半轴,B点在y轴正半轴上,
∴b=4,a=4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠OAB=45°
(2)解:①如图1,作EF⊥y轴于F,
∵B(0,4),H(0,1),
∴BH=OB﹣OH=4﹣1=3,
∵OA=OB=4,
∴△OAB为等腰直角三角形,
∴∠OBA=∠OAB=45°,
∴△BFE为等腰直角三角形,
∴BF=EF=2,
∴OF=OB﹣BF=4﹣1=3,
∴E(2,3),
∴E(2,3)为GH的中点,
∵S△BHE=3,
∴ ![]() BH×EF=3,即
BH×EF=3,即 ![]() ×3×EF=3,
×3×EF=3,
∴EF=2,
故点E到BH的距离为2.
②设G(m,n),则
∵BE为△BHG的中线,
∴ ![]() ,
, ![]() ,
,
解得m=4,n=5,
∴G点坐标为(4,5)
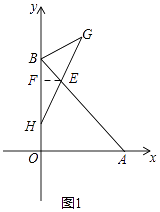
(3)解:如图2,过点B作BK⊥OC,交MN于点K,则∠KBO=∠DOA,
∵MN⊥AD,
∴∠DON+∠NOA=90°,
∴∠3+∠NOA=90°,
∵∠NOA+∠1=90°,
∴∠3=∠1,
在△KOB和△OAD中,
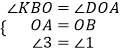 ,
,
∴△KOB≌△OAD(ASA),
∴KB=OD,∠2=∠7,
∵BC=OD,
∴KB=BC,
∵OB=OA,∠BOA=90°,
∴∠OBA=45°,
∴∠9=∠8=45°,
在△MKB和△MCB中,
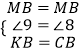 ,
,
∴△MKB≌△MCB(SAS),
∴∠6=∠5,
∵∠7+∠6=180°,
∴∠2+∠5=180°,即∠ADO+∠BCM=180°.
【解析】(1)根据非负数的性质,得出关于a、b的方程组,求得a、b即可得到A、B两点的坐标,最后利用等腰三角形的性质得出∠OAB的度数;(2)作EF⊥y轴于F,构造等腰直角三角形BEF,进而求出E点坐标,利用△BHE的面积即可得到点E到BH的距离;设G(m,n),根据BE为△BHG的中线,求得点G坐标即可;(3)过点B作BK⊥OC,交MN于点K,然后证明△OBK≌△OAD、△MKB≌△MCB,从而可证明∠ADO+∠BCM=180°.
【考点精析】掌握等腰直角三角形和三角形的面积是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
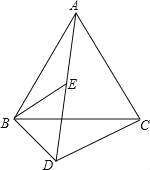
查看答案和解析>>【题目】如图,已知△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA﹣DB=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,
,  在数轴上对应的实数分别是
在数轴上对应的实数分别是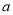 ,
, 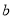 ,其中
,其中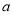 ,
, 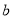 满足
满足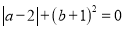 .
.(
 )求线段
)求线段 的长.
的长.(
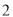 )点
)点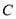 在数轴上对应的数为
在数轴上对应的数为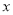 ,且
,且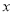 是方程
是方程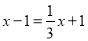 的解,在数轴上是否存在点
的解,在数轴上是否存在点 ,使
,使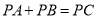 ?若存在,求出点
?若存在,求出点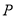 对应的数;若不存在,说明理由.
对应的数;若不存在,说明理由.(
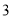 )在(
)在(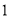 )和(
)和(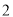 )的条件下,点
)的条件下,点 ,
, 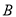 ,
, 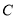 同时开始在数轴上运动,若点
同时开始在数轴上运动,若点 以每秒
以每秒 个单位长度是速度向左运动,点
个单位长度是速度向左运动,点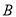 和点
和点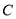 分别以每秒
分别以每秒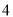 个单位长度和
个单位长度和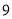 个单位长度的速度向右运动,点
个单位长度的速度向右运动,点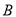 与点
与点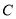 之间距离表示为
之间距离表示为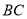 ,点
,点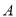 与点
与点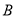 之间的距离表示为
之间的距离表示为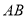 .设运动时间为
.设运动时间为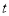 秒,试探究,随着时间
秒,试探究,随着时间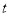 的变化,
的变化, 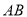 与
与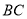 满足怎样的数量关系?请写出相应的等式.
满足怎样的数量关系?请写出相应的等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+1的图象与坐标轴的交点个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.

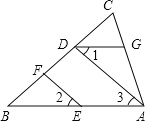
图⑴ 图⑵
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的自变量的取值范围是﹣3≤x≤6,相应函数的取值范围是﹣5≤y≤2,则一次函数的表达式为 .
-
科目: 来源: 题型:
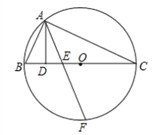
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,
(1)求证:AE平分∠DAO;
(2)若AB=6,AC=8,求OE的长.
相关试题

