搜索
【题目】已知一次函数y=kx+b的自变量的取值范围是﹣3≤x≤6，相应函数的取值范围是﹣5≤y≤2，则一次函数的表达式为 ．
参考答案：
【答案】y= 
x﹣ 
或y=﹣ x﹣ 
【解析】解：由题意得 
或 
， 解得 
或 
，
∴一次函数的表达式为y= x﹣ 或y=﹣ x﹣ ，
所以答案是y= x﹣ 或y=﹣ x﹣ ．
【考点精析】关于本题考查的一次函数的性质和确定一次函数的表达式，需要了解一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y＝x2﹣2x+1的图象与坐标轴的交点个数是( )
A.1B.2C.3D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B（0，b），点A（a，0）分别在y轴、x轴正半轴上，且满足
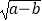+（b2﹣16）2=0．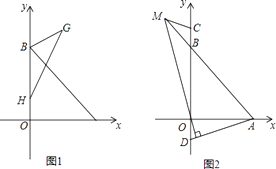 
（1）求A、B两点的坐标，∠OAB的度数；
（2）如图1，已知H（0，1），在第一象限内存在点G，HG交AB于E，使BE为△BHG的中线，且S△BHE=3，
①求点E到BH的距离；
②求点G的坐标；
（3）如图2，C，D是y轴上两点，且BC=OD，连接AD，过点O作MN⊥AD于点N，交直线AB于点M，连接CM，求∠ADO+∠BCM的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】按图填空，并注明理由．
⑴完成正确的证明：如图，已知AB∥CD，求证：∠BED=∠B+∠D
证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）
∴∠1= （ ）
∵AB∥CD（已知）
∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）
∴∠2= （ ）
又∠BED=∠1+∠2
∴∠BED=∠B+∠D （等量代换）．
⑵如图，在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
解：因为EF∥AD（已知）
所以∠2=∠3．（ ）
又因为∠1=∠2，所以∠1=∠3．（等量代换）
所以AB∥ （ ）
所以∠BAC+ =180°（ ）．
又因为∠BAC=70°，所以∠AGD=110°．
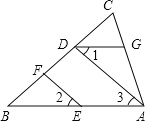
图⑴ 图⑵
-
科目： 来源： 题型：
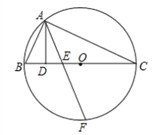
查看答案和解析>>【题目】如图，△ABC内接于⊙O，且BC是⊙O的直径，AD⊥BC于D，F是弧BC中点，且AF交BC于E，连接OA，
（1）求证：AE平分∠DAO；
（2）若AB=6，AC=8，求OE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB交CD于O，OE⊥AB．
（1）若∠EOD=20°，求∠AOC的度数；
（2）若∠AOC：∠BOC=1：2，求∠EOD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列图形中，不是轴对称图形的是 （）
A. 等边三角形 B. 等腰直角三角形 C. 四边形 D. 线段
相关试题
