【题目】如图,在△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线,若∠ABE![]() ∠C,AE:ED=2:1,则△BDE与△ABC的面积之比为( )
∠C,AE:ED=2:1,则△BDE与△ABC的面积之比为( )

A. 1:6 B. 1:9 C. 2:13 D. 2:15
参考答案:
【答案】D
【解析】
根据已知条件先求得S△ABE:S△BED=2:1,再根据三角形相似求得S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得.
S△BED,根据S△ABC=S△ABE+S△ACD+S△BED即可求得.
解:∵AD:ED=2:1,
∴AE:AD=2:3,
∵∠ABE=∠C,∠BAE=∠CAD,
∴△ABE∽△ACD,
∴S△ABE:S△ACD=4:9,
∴S△ACD=![]() S△ABE,
S△ABE,
∵AE:ED=2:1,
∴S△ABE:S△BED=2:1,
∴S△ABE=2S△BED,
∴S△ACD=![]() S△ABE=
S△ABE=![]() S△BED,
S△BED,
又∵S△ABC=S△ABE+S△ACD+S△BED=2S△BED+![]() S△BED+S△BED=
S△BED+S△BED=![]() S△BED.
S△BED.
∴△BDE与△ADC的面积比为2:15,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

-
科目: 来源: 题型:
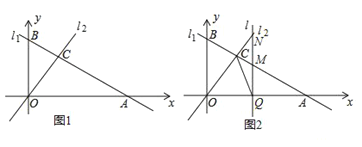
查看答案和解析>>【题目】如图1,直线l1:
 与坐标轴分别交于点A,B,与直线l2:
与坐标轴分别交于点A,B,与直线l2: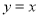 交于点C.
交于点C.(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒2个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=2MN时,求t的值;
②试探究是否存在点Q,使得以△OQC为等腰三角形?若存在,请直接写出t的值;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题的是( )
A.在△ABC中,若∠B+∠C=∠A,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c)(b﹣c),则△ABC是直角三角形
C.在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.在△ABC中,若a=32,b=42,c=52,则△ABC是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=4,BC=3,AB=5,AD为△ABC的角平分线,则CD的长度为( )

A.1B.
 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为执行“两免一补”政策,某地区2014年投入教育经费2500万元,预计到2016年,三年共投入8275万元.设投入教育经费的年平均增长率为x,那么下列方程正确的是( )
A. 2500x2
 8275 B. 2500(1+x%)2
8275 B. 2500(1+x%)2 8275
8275C. 2500(1+x)2
 8275 D. 2500+2500(1+x)+2500(1+x)2
8275 D. 2500+2500(1+x)+2500(1+x)2 8275
8275 -
科目: 来源: 题型:
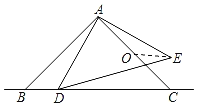
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,则OE的最小值是为( )
A.
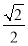 B.0.25C.1D.2
B.0.25C.1D.2
相关试题

