Question

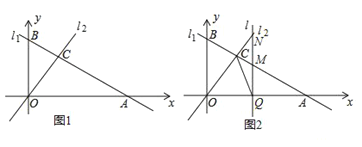
【题目】如图1,直线l1:与坐标轴分别交于点A,B,与直线l2:交于点C.

(1)求A，B两点的坐标；

(2)求△BOC的面积；

(3)如图2,若有一条垂直于x轴的直线l以每秒2个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s)，连接CQ.

①当OA=2MN时，求t的值；

②试探究是否存在点Q，使得以△OQC为等腰三角形?若存在，请直接写出t的值；若不存在，请说明理由

Answer 1

【答案】A(6,0)，B(0,3)；（2）△BOC的面积为3；（3）①t=1或t=3，②t=1,2,,

【解析】

（1）令x=0得到y=3，令y=0，得到x=6，从而可得A、B点的坐标；

（2）构建方程组确定点C坐标即可解决问题；

（3）①根据绝对值方程即可解决问题；

②分为三种情况，画出图形，根据等腰三角形的性质求出即可.

（1）对于直线，令x=0得到y=3，令y=0，得到x=6，

∴A（6，0），B（0，3）．

（2）由，解得，

∴C（2，2），

∴S△OBC=×3×2=3

（3）①设M（6-2t，-（6-2t）+3），N（6-2t，6-2t），

∴MN=|-（6-2t）+3-（6-2t）|=|3t-6|，

∵OA=2MN，

∴6=2|3t-6|，

解得t=1或3；

②分三种情况：

i）、CO为底时，Q为顶点时，如图①，

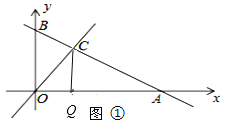
当∠COQ=45°，CQ=OQ，

∵C（2，2），

∴OQ=CQ=2，

∴AQ=OA-OQ=6-2=4，

∴t=4÷2=2(s)；

ii)当CO为腰时，C为顶点时，如图②，过C作CM⊥OA于M，

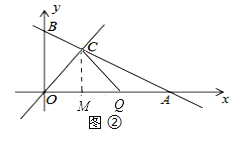
∵C（2，2），

∴CM=OM=2，

∴QM=OM=2，

∴AQ=OA-OQ=2，

∴t=2÷2=1(s)；

iii）当CO为腰时，O为顶点时，如图③：

OQ=OC=2，

AQ=AO-OQ=6-2或AQ=AO+OQ=6+2．

∴t=或t=.

综上所述：t的值为1或2或或．