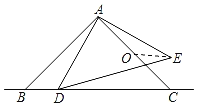
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,则OE的最小值是为( )
A.![]() B.0.25C.1D.2
B.0.25C.1D.2
参考答案:
【答案】A
【解析】
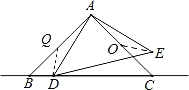
依题意设Q是AB的中点,连接DQ,先证得△AQD≌△AOE,得出QD=OE,根据点到直线的距离可知:当QD⊥BC时,QD最小,然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值,即可求得线段OE的最小值.
解:设Q是AB的中点,连接DQ,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵AB=AC=2,O为AC中点,
∴![]()
∴AQ=AO,
在△AQD和△AOE中,
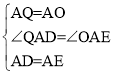 ,
,
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵点D在直线BC上运动,
∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∴![]()
∵QB=![]() AB=1,
AB=1,
∴![]()
∴线段OE的最小值是为![]() ;
;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线,若∠ABE
 ∠C,AE:ED=2:1,则△BDE与△ABC的面积之比为( )
∠C,AE:ED=2:1,则△BDE与△ABC的面积之比为( )
A. 1:6 B. 1:9 C. 2:13 D. 2:15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=4,BC=3,AB=5,AD为△ABC的角平分线,则CD的长度为( )

A.1B.
 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为执行“两免一补”政策,某地区2014年投入教育经费2500万元,预计到2016年,三年共投入8275万元.设投入教育经费的年平均增长率为x,那么下列方程正确的是( )
A. 2500x2
 8275 B. 2500(1+x%)2
8275 B. 2500(1+x%)2 8275
8275C. 2500(1+x)2
 8275 D. 2500+2500(1+x)+2500(1+x)2
8275 D. 2500+2500(1+x)+2500(1+x)2 8275
8275 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
-
科目: 来源: 题型:
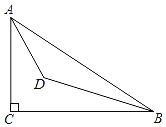
查看答案和解析>>【题目】如图,∠C=90°,AC=3,BC=4,∠ABC和∠BAC的角平分线的交点是点D,则△ABD的面积为_____.
相关试题

