【题目】在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 ![]() :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
(1)如图①,求证:BA=BP;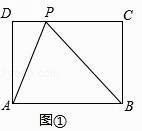
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求 ![]() 的值;
的值;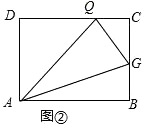
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.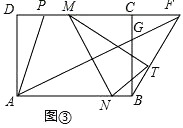
参考答案:
【答案】
(1)
证明:如图①中,设AD=BC=a,则AB=CD= ![]() a.
a.

∵四边形ABCD是矩形,
∴∠C=90°,
∵PC=AD=BC=a,
∴PB= ![]() =
= ![]() a,
a,
∴BA=BP
(2)
解:如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.
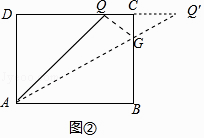
设AD=BC=QD=a,则AB=CD= ![]() a,
a,
∴CQ=CQ′= ![]() a﹣a,
a﹣a,
∵CQ′//AB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
(3)
证明:如图③中,作TH//AB交NM于H,交BC于K.
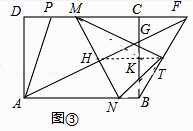
由(2)可知,AD=BC=1,AB=CD= ![]() ,DP=CF=
,DP=CF= ![]() ﹣1,
﹣1,
∵S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,
HT,
∵TH//AB//FM,TF=TB,
∴HM=HN,
∴HT= ![]() (FM+BN),
(FM+BN),
∵BN=PM,
∴HT= ![]() (FM+PM)=
(FM+PM)= ![]() PF=
PF= ![]() (1+
(1+ ![]() ﹣1)=
﹣1)= ![]() ,
,
∴S△MNT= ![]() HT=
HT= ![]() =定值
=定值
【解析】(1)如图①中,设AD=BC=a,则AB=CD= ![]() a.通过计算得出AB=BP=
a.通过计算得出AB=BP= ![]() a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD=
a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD= ![]() a,可得CQ=CQ′=
a,可得CQ=CQ′= ![]() a﹣a,由CQ′//AB,推出
a﹣a,由CQ′//AB,推出 ![]() =
= ![]() =
= ![]() =
= ![]() ;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT=
;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,利用梯形的中位线定理求出HT即可解决问题;
HT,利用梯形的中位线定理求出HT即可解决问题;
-
科目: 来源: 题型:
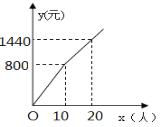
查看答案和解析>>【题目】某旅游风景区,门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上超过10人部分打b折.设团体游客
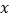 人,门票费用为y元,y与x之间的函数关系如图所示.
人,门票费用为y元,y与x之间的函数关系如图所示.(1)填空:a=_______;b=_________.
(2)请求出:当x>10时,
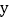 与
与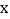 之间的函数关系式;
之间的函数关系式;(3)导游小王带A旅游团到该景区旅游,付门票费用2720元(导游不需购买门票),求A旅游团有多少人?
-
科目: 来源: 题型:
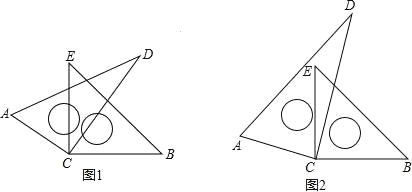
查看答案和解析>>【题目】如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)如图 1,若 CE 恰好是∠ACD 的角平分线,请你猜想此时 CD 是不是∠ECB 的角平分线?只回答出“是”或“不是”即可;
(2)如图 2,若∠ECD=α,CD 在∠BCE 的内部,请你猜想∠ACE 与∠DCB是否相等?并简述理由;
(3)在(2)的条件下,请问∠ECD 与∠ACB 的和是多少?并简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律: ①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表
成绩
7分
8分
9分
10分
人数
11
0
8
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=kx+b(k<0)与函数y=
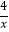 (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, 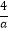 )、(c,
)、(c, 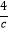 ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;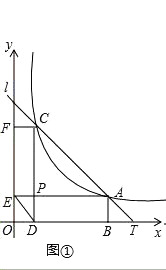
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;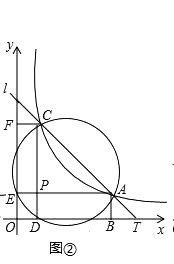
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.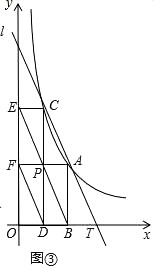
相关试题

