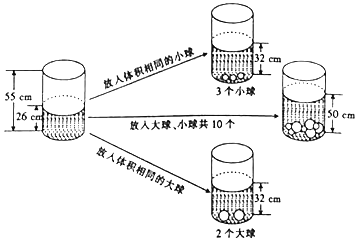
【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
参考答案:
【答案】(1) 2;3;(2)应该放入4个大球,6个小球
【解析】
(1)根据3个小球使水位升高了6cm,2个大球使水位升高了6cm进行解答;
(2)设应该放入x个大球,y个小球,根据图示中的等量关系列出方程组,并解答.
解:(1)依题意得:![]() =2(cm),
=2(cm),![]() =3(cm),
=3(cm),
即放入一个小球水面升高2cm,放入一个大球水面升高3cm.
故答案是:2;3.
(2)设应该放入x个大球,y个小球,
依题意得:![]() ,
,
解得![]() .
.
答:应该放入4个大球,6个小球
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各式分解因式
(1)

(2)x3+x2y-xy2-y3
(3)利用分解因式进行计算:3.46×14.7+0.54×14.7-29.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下内容:
已知实数m,n满足m+n=5,且
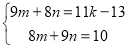 求k的值,
求k的值,三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于m,n的方程组
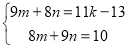 ,再求k的值、
,再求k的值、乙同学:将原方程组中的两个方程相加,再求k的值
丙同学:先解方程组
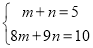 ,再求k的值
,再求k的值(1)试选择其中一名同学的思路,解答此题
(2)试说明在关于x、y的方程组
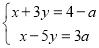 中,不论a取什么实数,x+y的值始终不变。
中,不论a取什么实数,x+y的值始终不变。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线 y13x 6与 x 轴、y 轴分别交于点 A,C;过点 C 的直线 y2x b 与 x 轴交于点 B.
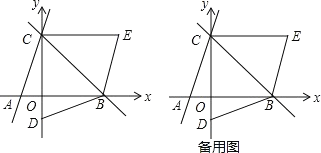
(1)b 的值为 ;
(2)若点 D 的坐标为(0,﹣2),将△BCD 沿直线 BC 对折后,点 D 落到第一象限的点 E 处, 求证:四边形 ABEC 是平行四边形;
(3)在直线 BC 上是否存在点 P,使得以 P、A、D、B 为顶点的四边形是平行四边形? 如果存在,请求出点 P 的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
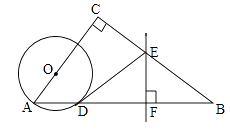
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
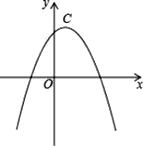
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
相关试题

