【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.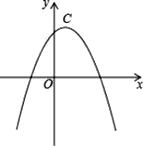
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
参考答案:
【答案】
(1)解:∵y1=﹣2x2+4x+2=﹣﹣2(x﹣1)2+4,
∴抛物线C1的顶点坐标为(1,4).
∵抛物线C1:与C2顶点相同,
∴ ![]() =1,﹣1+m+n=4.
=1,﹣1+m+n=4.
解得:m=2,n=3.
∴抛物线C2的解析式为u2=﹣x2+2x+3.
(2)解:如图1所示: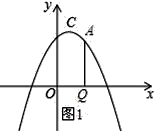
设点A的坐标为(a,﹣a2+2a+3).
∵AQ=﹣a2+2a+3,OQ=a,
∴AQ+OQ=﹣a2+2a+3+a=﹣a2+3a+3=﹣(a﹣ ![]() )2+
)2+ ![]() .
.
∴当a= ![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为 ![]() .
.
(3)解:如图2所示;连接BC,过点B′作B′D⊥CM,垂足为D.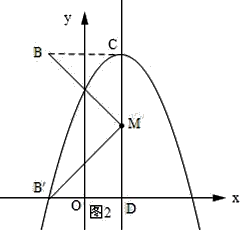
∵B(﹣1,4),C(1,4),抛物线的对称轴为x=1,
∴BC⊥CM,BC=2.
∵∠BMB′=90°,
∴∠BMC+∠B′MD=90°.
∵B′D⊥MC,
∴∠MB′D+∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中,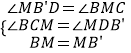 ,
,
∴△BCM≌△MDB′
∴BC=MD,CM=B′D.
设点M的坐标为(1,a).则B′D=CM=4﹣a,MD=CB=2.
∴点B′的坐标为(a﹣3,a﹣2).
∴﹣(a﹣3)2+2(a﹣3)+3=a﹣2.
整理得:a2﹣7a﹣10=0.
解得a=2,或a=5.
当a=2时,M的坐标为(1,2),
当a=5时,M的坐标为(1,5).
综上所述当点M的坐标为(1,2)或(1,5)时,B′恰好落在抛物线C2上.
【解析】解答此题抓住“友好抛物线”满足的条件是两条抛物线的顶点相同。
(1)先求出y1顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值。
(2) 抓住已知条件AQ⊥x轴,点Q在x轴上,设A(a,-a2+2a+3).则OQ=a,AQ=-a2+2a+3,然后得到OQ+AQ与a的函数关系式,最后利用配方法可求得OQ+AQ的最值。
(3)连接BC,过点B′作B′D⊥CM,垂足为D.先证明△BCM≌△MDB′,由全等三角形的性质得到BC=MD,CM=B′D,设点M的坐标为(1,a).则用含a的式子可表示出点B′的坐标,将点B′的坐标代入抛物线的解析式,建立方程可求得a的值,从而得到点M的坐标。
【考点精析】解答此题的关键在于理解因式分解法的相关知识,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
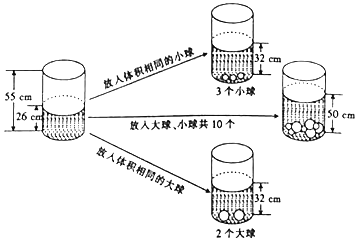
查看答案和解析>>【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线 y13x 6与 x 轴、y 轴分别交于点 A,C;过点 C 的直线 y2x b 与 x 轴交于点 B.
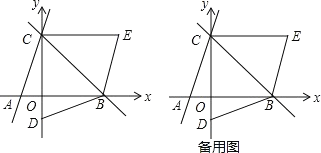
(1)b 的值为 ;
(2)若点 D 的坐标为(0,﹣2),将△BCD 沿直线 BC 对折后,点 D 落到第一象限的点 E 处, 求证:四边形 ABEC 是平行四边形;
(3)在直线 BC 上是否存在点 P,使得以 P、A、D、B 为顶点的四边形是平行四边形? 如果存在,请求出点 P 的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
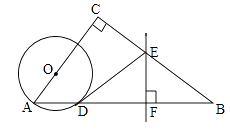
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )

A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是大于1的实数,且有a3+a-3=p,a3-a-3=q.
(1)若p+q=4,求p-q的值;
(2)当q2=22n+
 -2(n≥1,且n是整数)时,比较p与a3+
-2(n≥1,且n是整数)时,比较p与a3+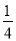 的大小.
的大小.
相关试题

