搜索
【题目】市教育局决定分别配发给一中8台电脑，二中10台电脑，但现在仅有12台，需
在商场购买6台. 从市教育局运一台电脑到一中、二中的运费分别是30元和50元，从商场
运一台电脑到一中、二中的运费分别是40元和80元. 要求总运费不超过840元，问有几
种调运方案？指出运费最低的方案。
参考答案：
【答案】见详解.
【解析】
设从教育局运往一中x台电脑，运往二中（12-x）台电脑，根据总运费不超过840元，列不等式求出x的取值范围．
设从教育局运往一中x台电脑,运往二中(12x)台电脑，
由题意得,30x+50(12x)+40(8x)+80(x2) 
840，
解得：2x4，
∵x为整数，
∴x=2，3，4，
有3种方案：从教育局运往一中2台，从商场运往一中6台，从教育局运往二中10台，从商场运往二中0台；
从教育局运往一中3台，从商场运往一中5台，从教育局运往二中9台，从商场运往二中1台；
从教育局运往一中4台，从商场运往一中4台，从教育局运往二中8台，从商场运往二中2台；
运费最少的方案为：第一种方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
分别交x轴、y轴于A、B两点，直线BC与x轴交于点
，P是线段AB上的一个动点
点P与A、B不重合
．
（1）求直线BC所对应的的函数表达式；
（2）设动点P的横坐标为t，
的面积为S．①求出S与t的函数关系式，并写出自变量t的取值范围；
②在线段BC上存在点Q，使得四边形COPQ是平行四边形，求此时点Q的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，
，D是AC的中点，过点A作直线
，过点D的直线EF交BC的延长线于点E，交直线l于点F，连接AE、CF．
（1）求证：①
≌
；②
；（2）若
，试判断四边形AFCE是什么特殊四边形，并证明你的结论；（3）若
，探索：是否存在这样的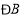
能使四边形AFCE成为正方形？若能，求出满足条件时的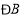的度数；若不能，请说明理由． -
科目： 来源： 题型：
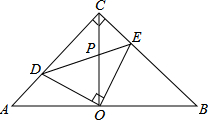
查看答案和解析>>【题目】如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D，E分别在直角边AC，BC上，且∠DOE=90°，DE交OC于点P．则下列结论：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面积等于四边形CDOE面积的2倍；(4)OD=OE．其中正确的结论有( )
A.
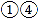B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】“九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话。
⑴现有1，2，3，4，5，6，7，8，9共九个数字，请将它们分别填入图1的九个方格中，使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15．
⑵通过研究问题⑴，利用你发现的规律，将3，5，－7，1，7，－3，9，－5，－1
这九个数字分别填入图2的九个方格中，使得横、竖、斜对角的所有三个数的和都相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下面的解题过程的横线上填空，并在括号内注明理由
.如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.
解：∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市数学调研小组对老师在讲评试卷中学生参与的深度与广度进行评价调查，其评价项目为“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”四项，该调研小组随机抽取了若干名初中七年级学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：
（1）在这次评价中，一共抽查了______名学生；
（2）请将频数分布直方图补充完整；
（3）如果全市有40000名七年级学生，那么在试卷评讲课中，“独立思考”的七年级学生约有多少人？
相关试题
