【题目】如图,直线![]() 分别交x轴、y轴于A、B两点,直线BC与x轴交于点
分别交x轴、y轴于A、B两点,直线BC与x轴交于点![]() ,P是线段AB上的一个动点
,P是线段AB上的一个动点![]() 点P与A、B不重合
点P与A、B不重合![]() .
.

(1)求直线BC所对应的的函数表达式;
(2)设动点P的横坐标为t,![]() 的面积为S.
的面积为S.
①求出S与t的函数关系式,并写出自变量t的取值范围;
②在线段BC上存在点Q,使得四边形COPQ是平行四边形,求此时点Q的坐标.
参考答案:
【答案】(1)y=2x+4;(2)①S=-2t+8(0<t<4);②点Q的坐标为(![]() ,
,![]() ).
).
【解析】
(1)根据函数表达式求出点B坐标,结合点C坐标求出BC的表达式;
(2)①根据三角形面积求法可得S与t的表达式;
②过点P作PQ∥x轴,交BC于点Q,得出P和Q的坐标,利用平行四边形的性质建立方程求解即可.
解:(1)直线y=-x+4与x轴、y轴交点坐标分别为A(4,0)、B(0,4)两点.
设直线BC所对应的函数关系式为y=kx+4.
∵直线BC经过点C(-2,0),
∴-2k+4=0,解得:k=2,
∴直线BC所对应的函数关系式为y=2x+4.
(2)①由题意,设点P的坐标为(t,-t+4),
∴S=S△POA=![]() ×OA×yP=
×OA×yP=![]() ×4×(-t+4)=-2t+8.
×4×(-t+4)=-2t+8.
即S=-2t+8(0<t<4).
②过点P作PQ∥x轴,交BC于点Q.
∵点P的坐标为(t,-t+4),
∴点Q的坐标为(![]() ,-t+4).
,-t+4).
∵四边形COPQ是平行四边形,
∴PQ=OC,即![]() .
.
解得:t=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列短文:
如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.

解答问题:
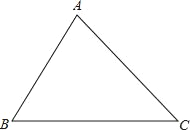
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4800米,甲从A地出发步行到B地,20分钟后乙从B地出发骑自行车到A地,设甲步行的时间为x分钟,甲、乙两人离A地的距离分别为
 米、
米、 米,
米, 、
、 与x的函数关系图象如图所示,根据图象解答下列问题:
与x的函数关系图象如图所示,根据图象解答下列问题:
(1)直接写出y
 、y
、y 与x的函数关系式,并写出自变量x的取值范围;
与x的函数关系式,并写出自变量x的取值范围;(2)求甲出发后多少分钟两人相遇,相遇时乙离A地多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,D是AC的中点,过点A作直线
,D是AC的中点,过点A作直线 ,过点D的直线EF交BC的延长线于点E,交直线l于点F,连接AE、CF.
,过点D的直线EF交BC的延长线于点E,交直线l于点F,连接AE、CF.
(1)求证:①
 ≌
≌ ;②
;② ;
;(2)若
 ,试判断四边形AFCE是什么特殊四边形,并证明你的结论;
,试判断四边形AFCE是什么特殊四边形,并证明你的结论;(3)若
 ,探索:是否存在这样的
,探索:是否存在这样的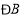 能使四边形AFCE成为正方形?若能,求出满足条件时的
能使四边形AFCE成为正方形?若能,求出满足条件时的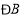 的度数;若不能,请说明理由.
的度数;若不能,请说明理由. -
科目: 来源: 题型:
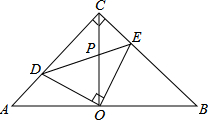
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】市教育局决定分别配发给一中8台电脑,二中10台电脑,但现在仅有12台,需
在商场购买6台. 从市教育局运一台电脑到一中、二中的运费分别是30元和50元,从商场
运一台电脑到一中、二中的运费分别是40元和80元. 要求总运费不超过840元,问有几
种调运方案?指出运费最低的方案。
相关试题

