【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点A的坐标: ;点B的坐标: ;
(2)若CD平分∠ACO,交x轴于D,求点D的坐标;
(3)在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求点E的坐标.

参考答案:
【答案】(1)(12,0),(12,9);(2)D(![]() ,0);(3)E(
,0);(3)E(![]() ,9).
,9).
【解析】
(1)根据矩形的性质即可解决问题;
(2)如图1中,作DM⊥AC于M.由Rt△CDO≌Rt△CDM(HL),推出CM=OC=9,由AC=![]() =15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
=15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.想办法求出直线EF的解析式即可解决问题;
解:(1)∵四边形OABC是矩形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9),
故答案为(12,0),(12,9);
(2)如图1中,作DM⊥AC于M.
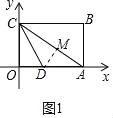
∵DC平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°,
∵CD=CD,
∴Rt△CDO≌△Rt△CDM(HL),
∴CM=OC=9,
∵AC=![]() =15,
=15,
∴AM=6,设OD=DM=m,
在Rt△ADM中,∵AD2=DM2+AM2,
∴x2+62=(12﹣x)2,
解得x=![]() ,
,
∴D(![]() ,0).
,0).
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.
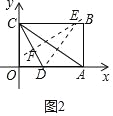
∵C(0,9),D(![]() ,0),
,0),
∴直线CD的解析式为y=﹣2x+9,
∴F(![]() ,
,![]() ),
),
∴直线EF的解析式为y=![]() x+
x+![]() ,
,
当y=9时,x=![]() ,
,
∴E(![]() ,9).
,9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB//CD,分别写出下列四个图形中,∠P与∠A、∠C的关系,请你从所得的四个关系中任选一个加以证明.

-
科目: 来源: 题型:
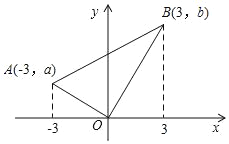
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB为直角,A(﹣3,a)、B(3,b),a+b﹣12=0,则△AOB的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示小王骑自行车和小李骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
(1)哪一个人出发早?早多长时间?哪一个人早到达目的地?早多长时间?
(2)求出两个人在途中行驶的速度是多少?
(3)分别求出表示自行车和摩托车行驶过程的函数关系式.

-
科目: 来源: 题型:
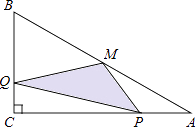
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
A.一直增大
B.一直减小
C.先减小后增大
D.先增大后减少 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动点A在函数
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 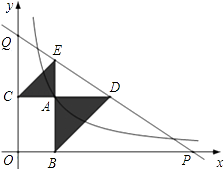
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是
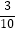 .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
相关试题

