【题目】如图,已知动点A在函数 ![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 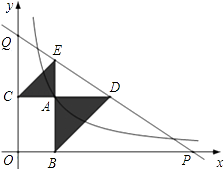
参考答案:
【答案】![]()
【解析】解: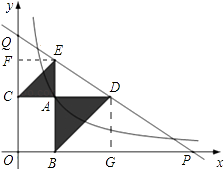
解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t, ![]() ),则AD=AB=DG=
),则AD=AB=DG= ![]() ,AE=AC=EF=t.
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE= ![]() ,
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP= ![]() .
.
又∵QE:DP=4:9,
∴ ![]() :
: ![]() =4:9,
=4:9,
解得t2= ![]() .
.
∴图中阴影部分的面积= ![]() AC2+
AC2+ ![]() AB2=
AB2= ![]() t2+
t2+ ![]() ×
× ![]() =
= ![]() +3=
+3= ![]() ;
;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t, ![]() ),
),
由AC=AE AD=AB,
∴AE=4t,AD= ![]() ,DG=
,DG= ![]() ,GP=9t,
,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t: ![]() =
= ![]() :9t,即t2=
:9t,即t2= ![]() ,
,
图中阴影部分的面积= ![]() ×4t×4t+
×4t×4t+ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示小王骑自行车和小李骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
(1)哪一个人出发早?早多长时间?哪一个人早到达目的地?早多长时间?
(2)求出两个人在途中行驶的速度是多少?
(3)分别求出表示自行车和摩托车行驶过程的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点A的坐标: ;点B的坐标: ;
(2)若CD平分∠ACO,交x轴于D,求点D的坐标;
(3)在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
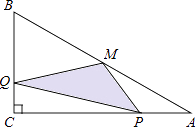
A.一直增大
B.一直减小
C.先减小后增大
D.先增大后减少 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是
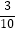 .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )
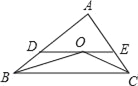
A. 3 B. 1 C. 2 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

相关试题

