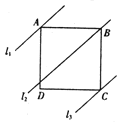
【题目】如图,四边形![]() 是正方形,直线
是正方形,直线![]() 分别过
分别过![]() 三点,且
三点,且![]() ,若
,若![]() 与
与![]() 的距离为6,正方形
的距离为6,正方形![]() 的边长为10,则
的边长为10,则![]() 与
与![]() 的距离为_________________.
的距离为_________________.
参考答案:
【答案】8
【解析】
画出l1到l2,l2到l3的距离,分别交l2,l3于E,F,通过证明△ABE≌△BCF,得出BF=AE,再由勾股定理即可得出结论.
过点A作AE⊥l1,过点C作CF⊥l2,

∴∠CBF+∠BCF=90°,
四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴∠ABE+∠CBF=90°,
∵l1∥l2∥l3,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
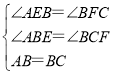 ,
,
∴△ABE≌△BCF(AAS),
∴BF=AE,
∴BF2+CF2=BC2,
∵正方形ABCD的面积为100,
∴CF2=100-62=64,
∴CF=8.
故答案为:8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A9m,0、Bm,0m0,以AB为直径的⊙M交y轴正半轴于点C,CD是⊙M的切线,交x轴正半轴于点D,过A作AECD于E,交⊙于F.
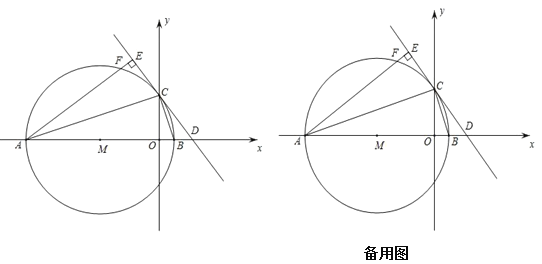
(1)求C的坐标;(用含m的式子表示)
(2)①请证明:EFOB;②用含m的式子表示AFC的周长;
(3)若
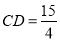 ,
,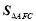 ,
,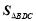 分别表示
分别表示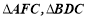 的面积,记
的面积,记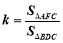 ,对于经过原点的二次函数
,对于经过原点的二次函数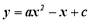 ,当
,当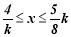 时,函数y的最大值为a,求此二次函数的解析式.
时,函数y的最大值为a,求此二次函数的解析式. -
科目: 来源: 题型:
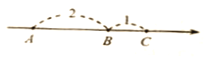
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示. 设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数为 、 ,p的值为 ;若以C为原点,p 的值为 ;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学实验室:
点A.B在数轴上分别表示有理数a.b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是 ,若AB=2,那么x为 ;
(3)当x是 时,代数式
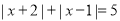 ;
;(4)若点A表示的数-1,点B与点A的距离是10,且点B在点A的右侧,动点P.Q同时从A.B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度。当PQ=1时,求运动时间?(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是
是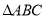 边
边 上的中点,
上的中点, ,垂足分别是点
,垂足分别是点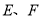 .
.(1)若
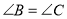 ,求证:
,求证: ;
;(2)若
 ,求证:四边形
,求证:四边形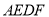 是矩形.
是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)12﹣(﹣16)+(﹣4)﹣5
(2)
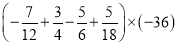
(3)
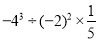
(4)(8a-7b)-(4a-5b)
(5)
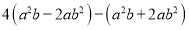
(6)先化简再求值,
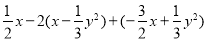 , 其中
, 其中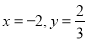
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD,求∠C.

相关试题

