【题目】如图(1),在![]() 和
和![]() 中,
中,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.

(1)求证:![]()
(2)如图(2),若![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() . ①求
. ①求![]() 的度数;
的度数;
②若![]() 平分
平分![]() ,试说明:
,试说明:![]() 平分
平分![]() .
.
参考答案:
【答案】(1)见解析;(2)①60°;②见解析;
【解析】
(1)由角平分线定义得出∠ACB=∠ECD,由SAS证明△ABC≌△EDC即可;
(2)①由SAS证明△BCF≌△DCG,得出∠CBF=∠CDG,在△BCF和△DHF中,由三角形内角和定理得出∠DHF=∠ACB=60°即可;
②由全等三角形的性质得出∠DEC=∠A,由三角形的外角性质得出∠ECM=∠2+∠1=60°,∠DCM=∠A+∠ABC=120°,得出∠A+∠ABC=2(∠2+∠1)=2∠2+2∠1=2∠2+∠A,即可得出结论.
(1)证明:∵CA平分∠BCE,
∴∠ACB=∠ECD,
在△ABC和△EDC中,

∴△ABC≌△EDC(SAS);
(2)①在△BCF和△DCG中, ,
,
∴△BCF≌△DCG(SAS);
∴∠CBF=∠CDG,
在△BCF和△DHF中,∵∠BFC=∠DFH,
∴∠DHF=∠ACB=60°;
②证明:如图(2)所示:
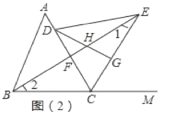
由(1)得:△ABC≌△EDC,
∴∠DEC=∠A,
∵∠ACB=∠ECD=60°,
∴∠ECM=60°,
∵EB平分∠DEC,
∴∠DEC=2∠1,
∵∠ECM=∠2+∠1=60°,∠DCM=∠A+∠ABC=120°,
∴∠A+∠ABC=2(∠2+∠1)=2∠2+2∠1=2∠2+∠A,
∴∠ABC=2∠2,
∴BE平分∠ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为________;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为________个单位长度.(在图形中标出点P)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形
 的两条直角边
的两条直角边 、
、 的长分别是
的长分别是 和
和 ,则此直角三角形外接圆半径为________
,则此直角三角形外接圆半径为________ ,内切圆半径为________
,内切圆半径为________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是等边三角形ABC的角平分线,E是BC延长线上的一点,且CE=CD,DF=BC,垂足为F.BF与EF相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
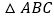 的边
的边 为直径画圆,与边
为直径画圆,与边 交于
交于 ,与边
,与边 交于
交于 ,已知
,已知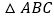 的面积是
的面积是 面积的
面积的 倍,
倍, 中有一个内角度数是另一内角度数的
中有一个内角度数是另一内角度数的 倍,试计算
倍,试计算 三个内角的度数:________.
三个内角的度数:________.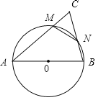
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知扇形
 中,
中, ,弦
,弦 ,点
,点 是弧
是弧 上任意一点(与端点
上任意一点(与端点 、
、 不重合),
不重合), 于点
于点 ,以点
,以点 为圆心、
为圆心、 长为半径作
长为半径作 ,分别过点
,分别过点 、
、 作
作 的切线,两切线相交于点
的切线,两切线相交于点 .
. 求弧
求弧 的长;
的长; 试判断
试判断 的大小是否随点
的大小是否随点 的运动而改变?若不变,请求出
的运动而改变?若不变,请求出 的大小;若改变,请说明理由.
的大小;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片
 中,
中,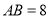 ,将纸片折叠,使顶点
,将纸片折叠,使顶点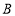 落在边
落在边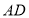 上的
上的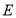 点处,折痕的一端
点处,折痕的一端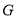 点在边
点在边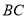 上.
上.(1)如图1,当折痕的另一端
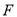 在
在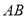 边上且
边上且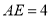 时,求
时,求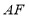 的长
的长(2)如图2,当折痕的另一端
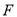 在
在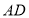 边上且
边上且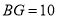 时,
时,①求证:
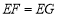 .②求
.②求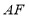 的长.
的长.(3)如图3,当折痕的另一端
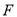 在
在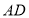 边上,
边上,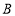 点的对应点
点的对应点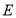 在长方形内部,
在长方形内部,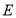 到
到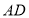 的距离为2
的距离为2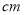 ,且
,且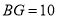 时,求
时,求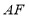 的长.
的长.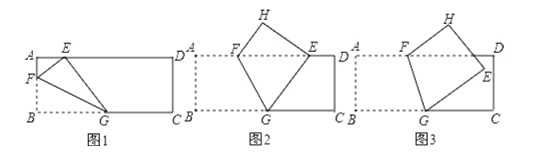
相关试题

