【题目】无锡阳山地区有A、B两村盛产水蜜桃,现A村有水蜜桃200吨,B村有水蜜桃300吨.计划将这些水蜜桃运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C,D两处的费用分别为每吨15元和18元.设从A村运往C仓库的水蜜桃重量为x吨,A、B两村运往两仓库的水蜜桃运输费用分别为yA元和yB元.
(1)请先填写下表,再根据所填写内容分别求出yA、yB与x之间的函数关系式;
收地运地 | C | D | 总计 |
A | x吨 | ______ | 200吨 |
B | ______ | ______ | 300吨 |
总计 | 240吨 | 260吨 | 500吨 |
(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的水蜜桃运费不得超过4830元,在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)当
;(2)当![]() 时,B村运费较少;当
时,B村运费较少;当![]() 时,A、B村运费一样;当
时,A、B村运费一样;当![]() 时,A村运费较少;(3)A村运50吨到C仓库,运150吨到D仓库,B村运190吨到C仓库,运110吨到D仓库;9580元.
时,A村运费较少;(3)A村运50吨到C仓库,运150吨到D仓库,B村运190吨到C仓库,运110吨到D仓库;9580元.
【解析】
(1)先设从A村运往C仓库的水蜜桃重量为x吨,就可以分别表示出A村到D处,B村到C处,B村到D处的数量.利用运送的吨数×每吨运输费用=总费用,列出函数解析式即可解答;
(2)由(1)中的函数解析式联立方程与不等式解答即可;
(3)首先由B村的水蜜桃的运费不得超过4830元得出不等式,再由两个函数和,根据自变量的取值范围,求得最值.
解:(1)A,B,两村运输水蜜桃情况如表,
收地运地 | C | D | 总计 |
A | x吨 | (200-x)吨 | 200吨 |
B | (240-x)吨 | (60+x)吨 | 300吨 |
总计 | 240吨 | 260吨 | 500吨 |
根据上表及题意,得
yA=20x+25(200x)=50005x,
yB=15(240x)+18(x+60)=3x+4680;
(2) ①当yA=yB时,即50005x=3x+4680,
解得x=40,
当x=40,两村的运费一样多,
②当yA>yB,即50005x>3x+4680,
解得x<40,
当0<x<40时,A村运费较高
③当yA<yB,,即50005x<3x+4680,
解得x>40,
当40<x≤200时,B村运费较高;
(3) ∵B村的水蜜桃运费不得超过4830元,
yB =3x+4680≤4830,
解得x≤50,
两村运费之和为yA+yB=50005x+3x+4680=96802x,
要使两村运费之和最小,所以x的值取最大时,运费之和最小
故当x=50时,最小费用是96802×50=9580(元)。
此时的调运方案为:
A村运50吨到C仓库,运150吨到D仓库,
B村运190吨到C仓库,运110吨到D仓库.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
(1)求证:AD=BE;
(2)设∠BPQ=α,那么α的大小是否随D、E的位置变化而变化?请说明理由;
(3)若PQ=3,PE=1,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
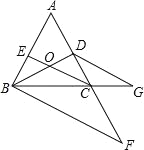
A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动1个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A2 019的坐标为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8,CB=6,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间。
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高
 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式; (2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
相关试题

