【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y= ![]() (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.﹣ ![]() ≤x≤1
≤x≤1
B.﹣ ![]() ≤x≤
≤x≤ ![]()
C.﹣ ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
参考答案:
【答案】B
【解析】当x=﹣10时,y= ![]() =﹣
=﹣ ![]() ;
;
当x=10时,y=﹣x+1=﹣9,
∴﹣9≤y1=y2≤﹣ ![]() .
.
设x1<x2,则y2=﹣x2+1、y1= ![]() ,
,
∴x2=1﹣y2,x1= ![]() ,
,
∴x1+x2=1﹣y2+ ![]() .
.
设x=1﹣y+ ![]() (﹣9≤y≤﹣
(﹣9≤y≤﹣ ![]() ),﹣9≤ym<yn≤﹣
),﹣9≤ym<yn≤﹣ ![]() ,
,
则xn﹣xm=ym﹣yn+ ![]() ﹣
﹣ ![]() =(ym﹣yn)(1+
=(ym﹣yn)(1+ ![]() )<0,
)<0,
∴x=1﹣y+ ![]() 中x值随y值的增大而减小,
中x值随y值的增大而减小,
∴1﹣(﹣ ![]() )﹣10=﹣
)﹣10=﹣ ![]() ≤x≤1﹣(﹣9)﹣
≤x≤1﹣(﹣9)﹣ ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】根据题目的已知条件,利用一次函数的性质和反比例函数的性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在反比例函数y=
 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=  的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 
A.6
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=
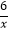 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )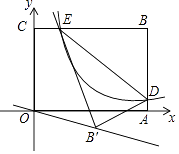
A.
B.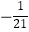
C.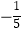
D.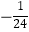
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
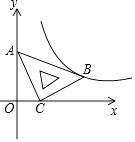
A.( ,0)
,0)
B.(2,0)
C.( ,0)
,0)
D.(3,0) -
科目: 来源: 题型:
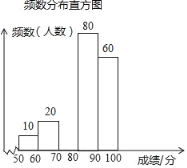
查看答案和解析>>【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
20
n
70≤x<80
m
0.15
80≤x<90
80
0.40
90≤x<100
60
0.30
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 和
和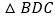 都是边长为1的等边三角形.
都是边长为1的等边三角形.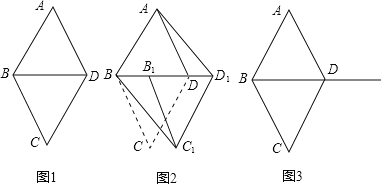
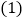 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?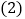 如图2,将
如图2,将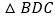 沿射线BD方向平移到
沿射线BD方向平移到 的位置,则四边形
的位置,则四边形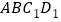 是平行四边形吗?为什么?
是平行四边形吗?为什么? 在
在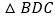 移动过程中,四边形
移动过程中,四边形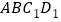 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离 写出过程
写出过程 ;如果不是,请说明理由
;如果不是,请说明理由 图3供操作时使用
图3供操作时使用 .
.
相关试题

