【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 
A.6
B.4
C.3
D.2
参考答案:
【答案】D
【解析】解:连接OA、OC、OD、OB,如图: 由反比例函数的性质可知S△AOE=S△BOF= ![]() |k1|=
|k1|= ![]() k1 , S△COE=S△DOF=
k1 , S△COE=S△DOF= ![]() |k2|=﹣
|k2|=﹣ ![]() k2 ,
k2 ,
∵S△AOC=S△AOE+S△COE ,
∴ ![]() ACOE=
ACOE= ![]() ×2OE=OE=
×2OE=OE= ![]() (k1﹣k2)…①,
(k1﹣k2)…①,
∵S△BOD=S△DOF+S△BOF ,
∴ ![]() BDOF=
BDOF= ![]() ×(EF﹣OE)=
×(EF﹣OE)= ![]() ×(3﹣OE)=
×(3﹣OE)= ![]() ﹣
﹣ ![]() OE=
OE= ![]() (k1﹣k2)…②,
(k1﹣k2)…②,
由①②两式解得OE=1,
则k1﹣k2=2.
故选D.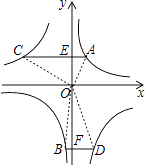
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在函数y1=﹣
 (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=
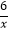 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )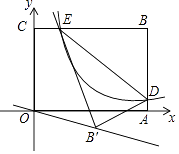
A.
B.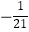
C.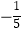
D.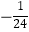
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y=
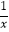 (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
A.﹣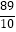 ≤x≤1
≤x≤1
B.﹣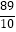 ≤x≤
≤x≤ 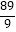
C.﹣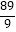 ≤x≤
≤x≤ 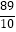
D.1≤x≤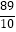
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
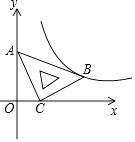
A.( ,0)
,0)
B.(2,0)
C.( ,0)
,0)
D.(3,0)
相关试题

