【题目】如图,△ABC是等腰直角三角形,且∠C=90°,直线l过C点.

(1)如图1,过A点、B点作直线l的垂线段AD、BE,垂足为D、E,请你探究AD、BE、DE满足的数量关系,并进行证明;
(2)当直线l绕点C旋转到如图2所示的位置时,请直接写出AD、BE和DE的数量关系(不用证明)
参考答案:
【答案】(1)DE=AD+BE,证明见解析;(2)DE=BEAD.
【解析】试题分析:(1)证△ACD≌△CBE,由全等三角形的性质可得出DC=EB,AD=CE,再结合DE=DC+CE即可得出DE=AD+BE;(2)同理得出△ACD≌△CBE,由全等三角形的性质可得出DC=EB,AD=CE,再结合DE=DC-CE即可得出DE=BE-AD.
解:(1)DE=AD+BE,证明:
∵△ABC是等腰直角三角形,
∴AC=BC.
∵∠ACB=90°,AD⊥直线l,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠ADC=∠CEB=90°,∠CAD=∠BCE,AC=CB,
∴△ACD≌△CBE(AAS),
∴DC=EB,AD=CE,
∴DE=DC+CE=AD+BE.
(2)DE=BEAD. 证明:
同(1)可证出△ACD≌△CBE,
∴DC=EB,AD=CE,
∴DE=DC-CE=BE-AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与
 轴、
轴、 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,F,E,C在同一直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC于E、F,若AB=CD,BD与EF互相平分吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年安徽全省生产总值比2017年增长8.02%,2017年比2016年增长8.5%.设安徽省这两年生产总值的年平均增长率为x,则所列方程正确的为( )
A. (1+x)2=8.02%×8.5%
B. (1+2x)2=8.02%×8.5%
C. (1+2x)2=(1+8.02%)×(1+8.5%)
D. (1+x)2=(1+8.02%)×(1+8.5%)
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在∠AOB的两边上截取AO=BO,CO=DO,连接AD,BC交于点P,那么在结论①△AOD≌△BOC ;②△APC≌△BPD;③点P在∠AOB的平分线上.其中正确的是 ( )
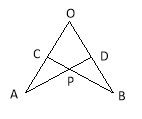
A.只有① B. 只有② C. 只有①② D.①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC中,AB=AC,D是BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:16a2﹣(a2+4)2=________.
相关试题

