【题目】已知等腰△ABC中,AB=AC,D是BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是 .
参考答案:
【答案】36°或45°.
【解析】
试题分析:△ACD和△ABD都是等腰三角形,但没有说具体的边相等,所以应分情况讨论.
(1)AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC=90°,那么∠C=45°;
(2)AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C=180°,那么∠C=36°.
解:应分两种情况:
(1)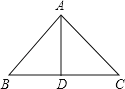
AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC=90°,那么∠C=45°;
(2)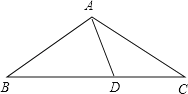
AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C=180°,那么∠C=36°.
故填36°或45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式﹣16x3+40x2y提出一个公因式﹣8x2后,另一个因式是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣
 、y=
、y=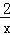 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )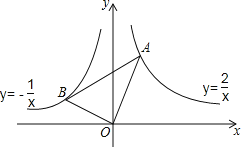
A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=4,x﹣y=﹣2,则x2﹣y2=__.
-
科目: 来源: 题型:
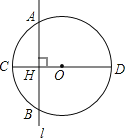
查看答案和解析>>【题目】如图,⊙O的半径OC=10cm,直线l⊥CO,垂足为H,交⊙O于A,B两点,AB=16cm,直线l平移多少厘米时能与⊙O相切?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=______.
相关试题

