【题目】在△ABC中,AB=AC,∠BAC=36°,将△ABC绕点A按逆时针旋转角度ɑ(0°<ɑ<180°)得到△ADE,连接CE、BD,BD与CE相交于点F。
(1)求证:BD=CE
(2)当ɑ等于多少度时,四边形AFDE是平行四边形?并说明理由。


参考答案:
【答案】(1)见解析;(2)当ɑ=108°时,四边形AFDE是平行四边形.
【解析】
(1)根据旋转的性质、全等三角形的判定定理证明△ABD≌△ACE,证明结论;
(2)根据平行四边形的判定定理证明.
(1)证明:∵△ADE是由△ABC旋转得到的,
∴AB=AD,AC=AE,∠BAD=∠CAE,
在△ABD和△ACE中

∴△ABD≌△ACE(SAS)
∴BD=CE
(2)当ɑ=108°时,四边形AFDE是平行四边形。
理由:
∵∠BAD=108°,AB=AD,
∴∠ABD=∠ADB=![]() (180°∠BAD)=36°
(180°∠BAD)=36°
∴∠DAE=∠ADB,
∴AE//FD,
又∵∠CAD=∠BAD-∠BAC=72°,
∴∠ADE=∠AED=![]()
∴∠CAD=∠ADE
∴AF//ED
∴四边形AFDE是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】a
 b是新规定的一种运算法则:a
b是新规定的一种运算法则:a b=a2+ab,例如3
b=a2+ab,例如3 (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.(1)求(﹣3)
 5的值;
5的值;(2)若(﹣2)
 x=6,求x的值;
x=6,求x的值;(3)若3
 (2
(2 x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细观察下面由“※”组成的图案和算式,解答问题:

1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+ … +19= ;
(2)请猜想:
1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)= ;
(3)请用上述规律计算:
103+105+107+ … +2013+2015
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A、B、C表示的数分别为﹣2、1、6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC

(1)请直接写出AB、BC、AC的长度;
(2)若点D从A点出发,以每秒1个单位长度的速度向左运动,点E从B点出发以每秒2个单位长度的速度向右运动,点F从C点出发以每秒5个单位长度的速度向右运动.设点D、E、F同时出发,运动时间为t秒,试探索:EF﹣DE的值是否随着时间t的变化而变化?请说明理由.
(3)若点M以每秒4个单位的速度从A点出发,点N以每秒3个单位的速度运动从C点出发,设点M、N同时出发,运动时间为t秒,试探究:经过多少秒后,点M、N两点间的距离为14个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习一元一次方程的解法时,我们经常遇到这样的试题:
“解方程:
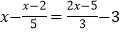 ”,请根据解题过程,在后面的括号内写出变形依据.
”,请根据解题过程,在后面的括号内写出变形依据.解:去分母,得 ( )
去括号,得 ( )
移项,得 ( )
合并,得 (合并同类项法则)
系数化为 1,得 ( )
请你写出在进行运算时容易出错的地方(至少写出三个).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.
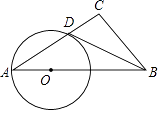
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一“过关游戏”,规定:在第n关要掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于
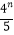 ,则算过关,否则不算过关.
,则算过关,否则不算过关.
(1)过第1关是事件(填“必然”、“不可能”或“不确定”,后同),过第4关是事件;
(2)当n=2时,计算过过第二关的概率(可借助表格或树状图).
相关试题

