【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
参考答案:
【答案】
(1)证明:∵△ABE是等边三角形,EF⊥AB,
∴∠EAF=60°,AE=BE,∠EFA=90°.
又∵∠ACB=90°,∠ABC=60°,
∴∠EFA=∠ACB,∠EAF=∠ABC.
在△ABC和△EAF中  ,
,
∴△ABC≌△EAF.
(2)解:结论:四边形EFDA是平行四边形.
理由:∵△ABC≌△EAF,
∴EF=AC.
∵△ACD是的等边三角形,
∴AC=AD,∠CAD=60°,
∴AD=EF.
又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=90°,
∴∠EFA=∠BAD=90°,
∴EF∥AD.
又∵EF=AD,
∴四边形EFDA是平行四边形
【解析】(1)由△ABE是等边三角形可知:AE=BE,∠EAF=60°,于是可得到∠EFA=∠ACB,∠EAF=∠ABC,接下来依据AAS证明△ABC≌△EAF即可;(2)由△ABC≌△EAF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD,然互再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.本题主要考查的是全等三角形的性质和判定、等边三角形的性质,证得∠EFA=∠BAD=90°是解题的关键.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2﹣
 x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
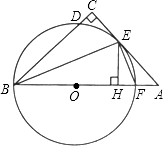
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
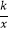 (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC. 
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校科技创新兴趣小组用他们设计的机器人,在平坦的操场上进行走展示.输入指令后,机器人从出发点A先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米到达终止点B.求终止点B与原出发点A的距离AB.
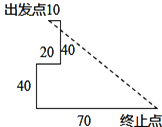
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师为了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)张老师一共调查了多少名同学?
(2)C类女生有多少名?D类男生有多少名?并将两幅统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”互助学习,请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在四边形ABCD的对角线BD所在的直线上,且BE=DF,AE∥CF,请再添加一个条件(不要在图中再增加其它线段和字母),能证明四边形ABCD是平行四边形,并证明你的想法.
你所添加的条件:____________________________________;
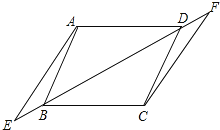
证明:
相关试题

