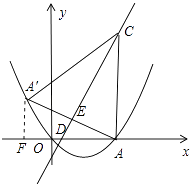
【题目】如图所示,抛物线y=ax2﹣ ![]() x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.
(1)求抛物线的解析式,并求出点C和点D的坐标;
(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;
(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.
参考答案:
【答案】
(1)
解:把点O(0,0),A(6,0)代入y=ax2﹣ ![]() x+c,得
x+c,得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x.
x.
当x=6时,y=2×6﹣2=10,
当y=0时,2x﹣2=0,解得x=1,
∴点C坐标(6,10),点D的坐标(1,0)
(2)
解:过点A′作AF⊥x轴于点F,
∵点D(1,0),A(6,0),可得AD=5,
在Rt△ACD中,CD= ![]() =5
=5 ![]() ,
,
∵点A与点A′关于直线y=2x﹣2对称,
∴∠AED=90°,
∴S△ADC= ![]() ×5
×5 ![]() AE=
AE= ![]() ×5×10,
×5×10,
解得AE=2 ![]() ,
,
∴AA′=2AE=4 ![]() ,DE=
,DE= ![]() =
= ![]() ,
,
∵∠AED=∠AFA′=90°,∠DAE=∠A′AF,
∴△ADE∽△AA′F,
∴ ![]() =
= ![]() =
= ![]() ,
,
解得AF=4,A′F=8,
∴OF=8﹣6=2,
∴点A′坐标为(﹣2,4),
当x=﹣2时,y= ![]() ×4﹣
×4﹣ ![]() ×(﹣2)=4,
×(﹣2)=4,
∴A′在抛物线上
(3)
解:∵点P在抛物线上,则点P(x, ![]() x2﹣
x2﹣ ![]() x),
x),
设直线A′C的解析式为y=kx+b,
∵直线A经过A′(﹣2,4),C(6,10)两点,
∴ ![]() ,解得
,解得 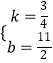 ,
,
∴直线A′C的解析式为y= ![]() x+
x+ ![]() ,
,
∵点Q在直线A′C上,PQ∥AC,点Q的坐标为(x, ![]() x+
x+ ![]() ),
),
∵PQ∥AC,又点Q在点P上方,
∴l=( ![]() x+
x+ ![]() )﹣(
)﹣( ![]() x2﹣
x2﹣ ![]() x)=﹣
x)=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
∴l与x的函数关系式为l=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,(﹣2<x≤6),
,(﹣2<x≤6),
∵l=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,l的最大值为
时,l的最大值为 ![]() .
.
【解析】(1)把O、A代入抛物线解析式即可求出a、c,令y=0,即可求出D坐标,根据A、C两点横坐标相等,即可求出点C坐标.(2)过点A′作AF⊥x轴于点F,求出A′F、FO即可解决问题.(3)设点P(x, ![]() x2﹣
x2﹣ ![]() x),先求出直线A′C的解析式,再构建二次函数,利用二次函数的性质即可解决问题.本题考查二次函数的综合题、待定系数法,最值问题等知识,解题的关键是灵活掌握二次函数的性质,学会构建二次函数解决问题最值问题,属于中考压轴题.
x),先求出直线A′C的解析式,再构建二次函数,利用二次函数的性质即可解决问题.本题考查二次函数的综合题、待定系数法,最值问题等知识,解题的关键是灵活掌握二次函数的性质,学会构建二次函数解决问题最值问题,属于中考压轴题.
【考点精析】掌握二次函数的最值是解答本题的根本,需要知道如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( )
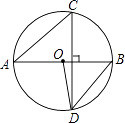
A.40°,80°
B.50°,100°
C.50°,80°
D.40°,100° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
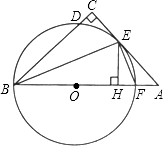
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
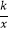 (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC. 
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.

(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
相关试题

