【题目】已知,如图,在![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
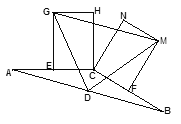
(1)求证:![]() 是等腰三角形。
是等腰三角形。
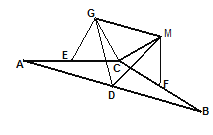
(2)如图,若将上图中的两个全等的矩形改为两个全等的正三角形(![]() 和
和![]() ),其他条件不变。请探究
),其他条件不变。请探究![]() 的形状,并说明理由。
的形状,并说明理由。
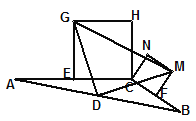
(3)若将上图中的两个全等的矩形改为两个正方形,并把![]() 中的边BC缩短到如图形状,请探究
中的边BC缩短到如图形状,请探究![]() 的形状,并说明理由。
的形状,并说明理由。
参考答案:
【答案】(1)证明见解析 (2)△DGM是等边三角形. (3)△DGM是等腰直角三角形.
【解析】试题分析:(1)先根据SAS证明△FBM≌△MDH,得到DG=DM,即![]() 是等腰三角形;(2)类似先证
是等腰三角形;(2)类似先证![]() 是等腰三角形,再求GM=GD,从而得出
是等腰三角形,再求GM=GD,从而得出![]() 是等边三角形;(3)类似(1)(2)中方法,先得到
是等边三角形;(3)类似(1)(2)中方法,先得到![]() 是等腰三角形,再求∠GDM=∠GEC=900,从而得出
是等腰三角形,再求∠GDM=∠GEC=900,从而得出![]() 是等腰直角三角形;
是等腰直角三角形;
试题解析:
(1)证明:∵四边形CEGH和CFMN是全等的矩形,
∴CE= CF,EG=FM,∠GEC =∠MFC = 90°.
连接DE、DF,如图.
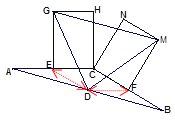
∵D、E、F分别是AB、AC、BC的中点,
DE∥BC,且DE=CE =![]() BC;
BC;
DF∥AC,且DF = CE = ![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,
∴∠DEG=∠DFM.
∵AC=BC,
∴DE=DF.
∴△FBM≌△MDH(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
(2)△DGM是等边三角形.
证明:∵![]() 和
和![]() 是全等的等边三角形,
是全等的等边三角形,
∴CE=EG=CG=CF=FM=CM,∠GEC=∠MFC=60°.
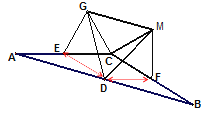
连接DE、DF,如图.
∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,且DE =CE =![]() BC;
BC;
DF∥AC,且DF=CE=![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,
∴∠DEG=∠DFM.
∵AC=BC,
∴DE=DF.
∴△FBM≌△MDH(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
又∵∠GCM+∠ACB=3600-600-600=2400
∠GED+∠ACB=∠GEC+∠CED+∠ACB=600+1800=2400
∴∠GCM=∠GED
又DE=CF=CM,EG=CG
∴△GED≌△GCM(SAS).
∴GM=GD
∴△DGM是等边三角形.
(3)△DGM是等腰直角三角形.
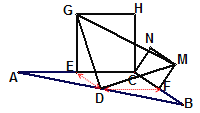
显然,由(1)(2)易得△GED≌△DFM(SAS)
∴DG=DM,∠DGE=∠MDF
∵DF∥AC
∴∠CED+∠EDF=1800/p>
即:∠CED+∠EDG+∠GDM+∠MDF=1800
又由三角形内角和可知∠CED+∠EDG+∠GEC+∠DGE=1800
∴∠GDM=∠GEC=900
∴△DGM是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式与2x2+x+1的和等于2x2+3x﹣1,则此多项式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.
(1)求证:CQ=QP
(2)设点Q的坐标为(x,y),求y关于x的函数关系式及自变量x的取值范围;
(3)如图2,连结OQ,OB,当点P在线段OA上运动时,设三角形OBQ的面积为S,当x取何值时,S取得最小值,并求出最小值;
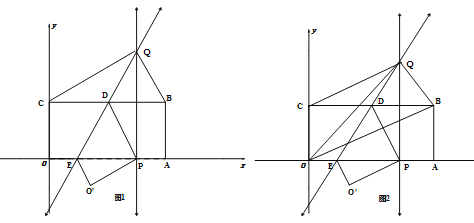
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.
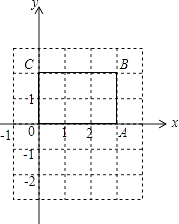
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2:3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为解决大班额问题,对学校进行扩建,计划用三年时间对全县学校进行扩建和改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20%、﹣220%B. 40%C. ﹣220%D. 20%
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件)
P=45﹣x
销售单价q(元/件)
当1≤x≤18时,q=20+x
当18<x≤30时,q=38
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠ABC=70,∠CDE=140,则∠BCD的值为( )
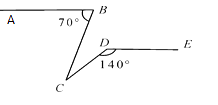
A.70
B.50
C.40
D.30
相关试题

