【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件) | P=45﹣x |
销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
参考答案:
【答案】(1)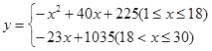 (2)在这30天中,该超市销售这种商品,第18天的利润最大,且最大利润为621元.
(2)在这30天中,该超市销售这种商品,第18天的利润最大,且最大利润为621元.
【解析】试题分析:(1)根据总价=单价×数量,分别用每件商品的利润乘以这种商品的销售量,求出y关于x的函数关系式即可.
(2)首先分类讨论,求出①当1≤x≤18时,②当18<x≤30时,该超市销售这种商品所获的利润是多少,然后比较大小,判断出该超市销售这种商品第几天的利润最大,最大利润是多少即可;
试题解析:
(1)①当1≤x≤18时,
y=(20+x﹣15)(45﹣x)
=(5+x)(45﹣x)
=﹣x2+40x+225
②当18<x≤30时,
y=(38﹣15)(45﹣x)
=23(45﹣x)
=﹣23x+1035
∴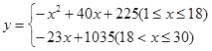
(2)①当1≤x≤18时,y=﹣(x﹣20)2+625,
∴当x=18时,y最大值=621元.
②当18<x≤30时,
∵﹣30<0,
∴y随x的增大而减小,
又∵x取正整数,
∴当x=19时,y最大值=598(元).
∵621>598,
∴在这30天中,该超市销售这种商品,第18天的利润最大,且最大利润为621元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.
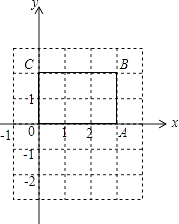
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2:3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在
 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。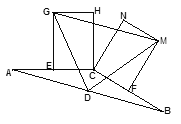
(1)求证:
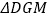 是等腰三角形。
是等腰三角形。(2)如图,若将上图中的两个全等的矩形改为两个全等的正三角形(
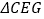 和
和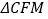 ),其他条件不变。请探究
),其他条件不变。请探究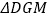 的形状,并说明理由。
的形状,并说明理由。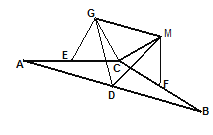
(3)若将上图中的两个全等的矩形改为两个正方形,并把
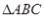 中的边BC缩短到如图形状,请探究
中的边BC缩短到如图形状,请探究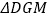 的形状,并说明理由。
的形状,并说明理由。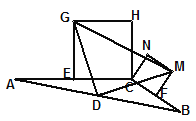
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为解决大班额问题,对学校进行扩建,计划用三年时间对全县学校进行扩建和改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20%、﹣220%B. 40%C. ﹣220%D. 20%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠ABC=70,∠CDE=140,则∠BCD的值为( )
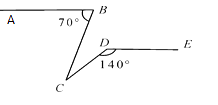
A.70
B.50
C.40
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式a2b2+6ab+A是完全平方式,则A=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=(m+1)x|m|+1+4x﹣5是二次函数,则m= .
相关试题

