【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.
(1)求证:CQ=QP
(2)设点Q的坐标为(x,y),求y关于x的函数关系式及自变量x的取值范围;
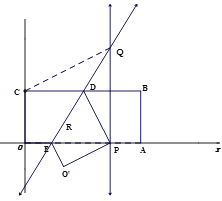
(3)如图2,连结OQ,OB,当点P在线段OA上运动时,设三角形OBQ的面积为S,当x取何值时,S取得最小值,并求出最小值;
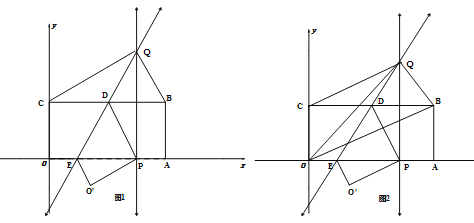
参考答案:
【答案】(1)CQ=PQ(2)![]() (3)
(3)![]()
【解析】试题分析:(1)由CD=PD,∠CDE=∠PDE得到∠CDQ=∠PDQ,再加上DQ=DQ可得△CDQ≌△PDQ,所以得CQ=PQ;(2)由Q(x,y) ,则CQ=PQ=y,设QP交BC于H,则QH=y-2,CH=x,由勾股定理,得![]() ,所以
,所以![]() ;(3)设直线OB与直线PQ相交于点G(x,y),则
;(3)设直线OB与直线PQ相交于点G(x,y),则![]() ,所以
,所以![]() ,所以
,所以![]() ,即当x=1时,S有最小值为
,即当x=1时,S有最小值为![]() ;
;
试题解析:
(1)由已知易得CD=PD,∠CDE=∠PDE
∴ ∠CDQ=∠PDQ
又∵DQ=DQ
∴△CDQ≌△PDQ
得CQ=PQ
(2)∵Q(x,y)
CQ=PQ=y
设QP交BC于H,则QH=y-2,CH=x,由勾股定理,得


(3)设直线OB与直线PQ相交于点G(x,y),则易得![]()
![]() .
.
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排査和处置.在疫情排査过程中.某农场第一天发现3头生猪发病.两天后发现共有363头生猪发病,求每头发病生猪平均每天传染多少头生猪?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
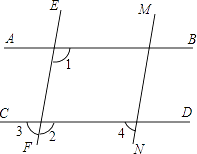
(1)已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式与2x2+x+1的和等于2x2+3x﹣1,则此多项式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.
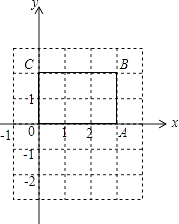
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2:3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在
 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。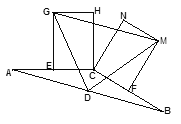
(1)求证:
 是等腰三角形。
是等腰三角形。(2)如图,若将上图中的两个全等的矩形改为两个全等的正三角形(
 和
和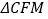 ),其他条件不变。请探究
),其他条件不变。请探究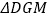 的形状,并说明理由。
的形状,并说明理由。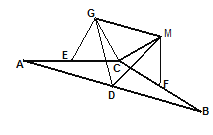
(3)若将上图中的两个全等的矩形改为两个正方形,并把
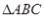 中的边BC缩短到如图形状,请探究
中的边BC缩短到如图形状,请探究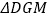 的形状,并说明理由。
的形状,并说明理由。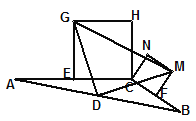
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为解决大班额问题,对学校进行扩建,计划用三年时间对全县学校进行扩建和改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20%、﹣220%B. 40%C. ﹣220%D. 20%
相关试题

