【题目】在直角坐标系中将下列各点用线段依次连结起来,能得到什么图案?
(0,0),(-4,-2),(-3,0),(-5,-1),(-5,1),(-3,0),(-4,2),(0,0).
(1)若以上各点纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连结起来,所得的图案与原来的图案相比有什么变化?若横坐标不变,纵坐标分别加3呢?
(2)连结点(3,3),(-1,1),(0,3),(-2,2),(-2,4),(0,3),(-1,5),(3,3),观察所得图案和原图案的位置关系.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)作出平面直角坐标系并描出各点然后连接,再根据平移的性质解答即可;
(2)在平面直角坐标系中找出各点的位置,然后解答即可.
将(0,0),(-4,-2),(-3,0),(-5,-1),(-5,1),(-3,0),(-4,2),(0,0)各点用线段依次连结起来,如图①,得到的图案是条鱼.
(1)若纵坐标保持不变,横坐标分别加3,得到的坐标分别是(3,0),(-1,-2),(0,0),(-2,-1),(-2,1),(0,0),(-1,2),(3,0),用线段依次连结起来,如图②,所得的图案依然是一条鱼,与原来的图案相比,形状、大小不变,只是向右平移了3个单位;若横坐标不变,纵坐标分别加3,得到的坐标分别是(0,3),(-4,1),(-3,3),(-5,2),(-5,4),(-3,3),(-4,5),(0,3),用线段依次连结起来,如图③,与原来的图案相比,形状、大小不变,只是向上平移了3个单位.
(2)连结点(3,3),(-1,1),(0,3),(-2,2),(-2,4),(0,3),(-1,5),(3,3),如图④,由观察可知此图案是由原图案先向上平移了3个单位,再向右平移了3个单位得到的.
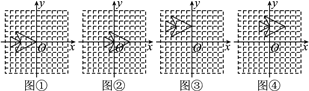
-
科目: 来源: 题型:
查看答案和解析>>【题目】长为8,宽为4的长方形在平面直角坐标系中的位置如图所示,动点P从(0,3)点出发,沿图中所示的箭头方向运动,到(3,0)点时记为第一次反弹,以后每当碰到长方形的边时记一次反弹,反弹时反射角等于入射角,那么点P第2018次反弹时碰到长方形边上的点的坐标为( )

A. (1,4) B. (8,3) C. (7,4) D. (3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)
(1)A点到原点O的距离是 。
(2)将点C向
 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。(3)连接CE,则直线CE与
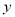 轴是什么关系?
轴是什么关系?(4)点F分别到
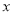 、
、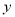 轴的距离是多少?
轴的距离是多少?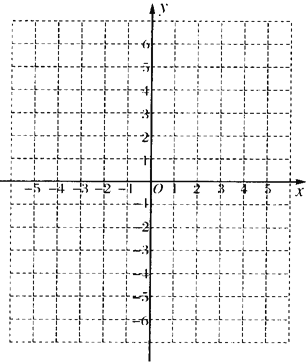
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
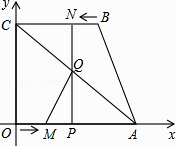
(1)点(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;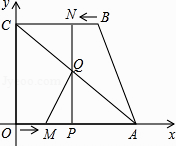
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)实验与探究
①在下列三个图中,给出菱形ABCD的顶点A,B,D的坐标(如图所示),写出图(1),(2),(3)中点C的坐标,它们分别是、、;
②菱形绕原点逆时针依照(90°,2)旋转后点C对应的点C1的坐标分别是、、 . (其中(90°,2)表示旋转90°,长度扩大2倍)
(2)归纳与发现
①在图4中,给出菱形ABCD的顶点A,B,D的坐标,求出顶点C的坐标;(点C的坐标用含a,b,c,d,e,f的代数式表示)
②菱形绕原点逆时针依照(90°,2)旋转后对应的C1的坐标为多少.
(3)运用与推广
①通过对图(1),(2),(3),(4)的观察和顶点C的坐标的探究,你会发现:无论菱形ABCD处于直角坐标系的哪个位置,当顶点坐标为:A(a,b),B(c,d),C(m,n),D(e,f)时,四个顶点的横坐标a,c,m,e之间的等量关系为;纵坐标b,d,n,f之间的等量关系为(不必证明);
②通过顶点C的坐标和旋转后的C1的坐标探究,你会发现无论C点在哪个位置,绕原点逆时针依照(90°,n)旋转,设C(x1 , y1),C1(x2 , y2),则x1 , x2 , y1 , y2满足的等式是(不必证明).
(备注:有两点A(x1 , y1),B(x2 , y2),则它们的中点P的坐标为( ,
,  ))
))
相关试题

