【题目】解答题
(1)实验与探究
①在下列三个图中,给出菱形ABCD的顶点A,B,D的坐标(如图所示),写出图(1),(2),(3)中点C的坐标,它们分别是、、;
②菱形绕原点逆时针依照(90°,2)旋转后点C对应的点C1的坐标分别是、、 . (其中(90°,2)表示旋转90°,长度扩大2倍)
(2)归纳与发现
①在图4中,给出菱形ABCD的顶点A,B,D的坐标,求出顶点C的坐标;(点C的坐标用含a,b,c,d,e,f的代数式表示)
②菱形绕原点逆时针依照(90°,2)旋转后对应的C1的坐标为多少.
(3)运用与推广
①通过对图(1),(2),(3),(4)的观察和顶点C的坐标的探究,你会发现:无论菱形ABCD处于直角坐标系的哪个位置,当顶点坐标为:A(a,b),B(c,d),C(m,n),D(e,f)时,四个顶点的横坐标a,c,m,e之间的等量关系为;纵坐标b,d,n,f之间的等量关系为(不必证明);
②通过顶点C的坐标和旋转后的C1的坐标探究,你会发现无论C点在哪个位置,绕原点逆时针依照(90°,n)旋转,设C(x1 , y1),C1(x2 , y2),则x1 , x2 , y1 , y2满足的等式是(不必证明).
(备注:有两点A(x1 , y1),B(x2 , y2),则它们的中点P的坐标为( ![]() ,
, ![]() ))
))
参考答案:
【答案】
(1)(8,4);(e+c,d);(c+e﹣a,d);(﹣8,16);(﹣2d,2e+2c);(﹣2d,2c+2e﹣2a)
(2)
解:①如图所示:分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,
分别过A,D作AE⊥BB1于E,DF⊥CC1于点F.

在平行四边形ABCD中,CD=BA,
又∵BB1//CC1,
∴∠EBA+∠ABC+∠BCF=∠ABC+∠BCF+∠FCD=180度.
∴∠EBA=∠FCD.
在△BEA和△CFD中
 ,
,
∴△BEA≌△CFD(AAS).
∴AE=DF=a﹣c,BE=CF=d﹣b.
设C(x,y).
由e﹣x=a﹣c,得x=e+c﹣a.
由y﹣f=d﹣b,得y=f+d﹣b.
∴C(e+c﹣a,f+d﹣b).
②菱形绕原点逆时针依照(90°,2)旋转后对应的C1的坐标为(2b﹣2f﹣2d,2e+2c﹣2a)
(3)m=c+e﹣a;n=d+f﹣b;x2=﹣ny1 , y2=nx1
【解析】解:(1.)①由题意可得出:图1,图2,图3中的顶点C的坐标,它们分别是(8,4),(e+c,d),(c+e﹣a,d).
所以答案是:(8,4),(e+c,d),(c+e﹣a,d).
②菱形绕原点逆时针依照(90°,2)旋转后点C对应的点C1的坐标分别是(﹣8,16),(﹣2d,2e+2c),(﹣2d,2c+2e﹣2a)
所以答案是(﹣8,16),(﹣2d,2e+2c),(﹣2d,2c+2e﹣2a).
(3.)①由图1,2,3可得出:m=c+e﹣a,n=d+f﹣b.或m+a=c+e,n+b=d+f.
所以答案是:m=c+e﹣a,n=d+f﹣b.
②由图1,2,3可得出:无论C点在哪个位置,绕原点逆时针依照(90°,n)旋转可得:x2=﹣ny1 , y2=nx1 ,
所以答案是x2=﹣ny1 , y2=nx1 .
【考点精析】掌握菱形的性质和图形的旋转是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中将下列各点用线段依次连结起来,能得到什么图案?
(0,0),(-4,-2),(-3,0),(-5,-1),(-5,1),(-3,0),(-4,2),(0,0).
(1)若以上各点纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连结起来,所得的图案与原来的图案相比有什么变化?若横坐标不变,纵坐标分别加3呢?
(2)连结点(3,3),(-1,1),(0,3),(-2,2),(-2,4),(0,3),(-1,5),(3,3),观察所得图案和原图案的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
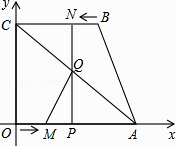
(1)点(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;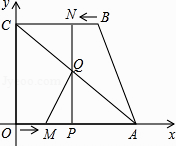
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
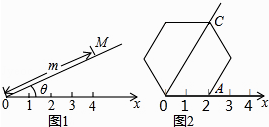
A.(60°,4)
B.(45°,4)
C.(60°,2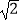 )
)
D.(50°,2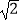 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣  x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( ) 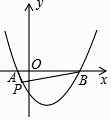
A.﹣1<m<0
B.﹣1<m<0或3<m<4
C.0<m<3或m>4
D.m<﹣1或0<m<3
相关试题

