【题目】某县某中学开展“庆五四”歌咏比赛活动,八年级(1)、(2)班各选出5名选手参加比赛,两个班选出的5名选手的比赛成绩(满分为100分)如图所示.

(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
八(1) | ________________ | 85 |
八(2) | 80 | ________________ |
(2)请你计算八(1)和八(2)班的平均成绩各是多少分.
(3)结合两班比赛成绩的平均数和中位数,分析哪个班级的比赛成绩较好.
(4)请计算八(1)、八(2)班的比赛成绩的方差,并说明哪个班的成绩比较稳定.
参考答案:
【答案】(1)85,100;(2)八(1)的平均分为:85(分),八(2)的平均分为:85(分);(3)八(1)班成绩好些;(4)![]() 班=70,
班=70,![]() 班=160,八(1)班成绩稳定.
班=160,八(1)班成绩稳定.
【解析】
(1)观察统计图分别写出八(1)班和八(2)班5名选手的比赛成绩,然后根据中位数和众数的定义求解即可;
(2)根据平均数公式计算即可;
(3)在平均数相同的情况下,中位数较高的成绩较好;
(4)先根据方差公式分别计算两个班比赛成绩的方差,再根据方差的意义判断即可.
解:(1)将八(1)班5名选手的比赛成绩从小到大排列为75,80,85,85,100,中间的数据为85,所以中位数为85.
八(2)班5名选手的比赛成绩为70,100,100,75,80,
其中数据100出现了两次,次数最多,所以众数是100;
(2)八(1)的平均分为:![]() (分),
(分),
八(2)的平均分为:![]() (分);
(分);
(3)八(1)班成绩好些.
因为两个班级的平均数都相同,八(1)班的中位数高,所以在平均数相同的情况下中位数高的八(1)班成绩好.
(4)![]()
![]() ,
,
![]()
![]() ,
,
∵![]() ,
,
∴八(1)班成绩稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数
第2排的座位数
第3排的座位数
…
第
 排的座位数
排的座位数12
14
16
…
(2)影院最后两排共有多少个座位?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一振子从点A开始左右来回振动8次,如果规定向右为正,向左为负,这8次振动的记录为(单位:mm):+10,-9,+8,-6,+7.5,-6,+8,-7.
(1)求该振子停止时所在的位置距A点多远?
(2)如果每毫米需用时间0.02 s,则完成8次振动共需要多少秒?
-
科目: 来源: 题型:
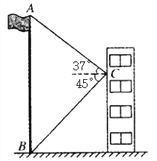
查看答案和解析>>【题目】如图,在教学楼距地面8米高的窗口中C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°.升旗时,国旗上端悬挂在距地面2米处.若国旗随国歌声冉冉升起,并在国歌播放40秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有任意一点
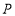 和
和 ,按要求解答下列问题:
,按要求解答下列问题:(1)当点
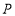 和
和 外部时,如图①,过点
外部时,如图①,过点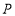 作
作 ,
,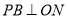 ,垂足分别为
,垂足分别为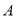 、
、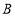 ,量一量
,量一量 和
和 的度数,用数学式子表达它们之间的数量关系 ;
的度数,用数学式子表达它们之间的数量关系 ;(2)当点
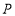 在
在 内部时,如图②,以点
内部时,如图②,以点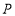 为顶点作
为顶点作 ,使
,使 的两边分别和
的两边分别和 的两边垂直,垂足分别为
的两边垂直,垂足分别为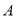 、
、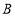 ,用数学式子写出
,用数学式子写出 和
和 的数量关系;
的数量关系;(3)由上述情形,用文字语言叙述结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 .
(4)在图②中,若
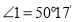 ,求
,求 的度数.
的度数.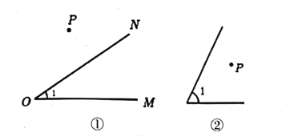
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
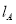 ,
,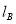 分别表示小明步行与小刚骑车在同一路上行驶的路程S与时间t的关系.
分别表示小明步行与小刚骑车在同一路上行驶的路程S与时间t的关系.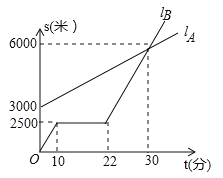
(1)小刚出发时与小明相距________米.走了一段路后,自行车发生故障进行修理,所用的时间是________分钟.
(2)求出小明行走的路程S与时间t的函数关系式.(写出计算过程)
(3)请通过计算说明:若小刚的自行车不发生故障,保持出发时的速度前进,何时与小明相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,直线y=12x+2与
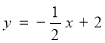 交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.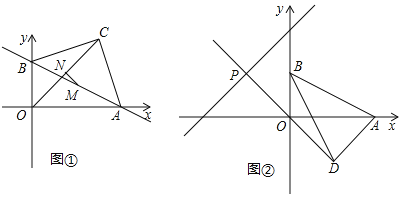
(1)求线段AB的长度
(2)求直线BC的解析式;
(3)如图②,将线段AB绕B点沿顺时针方向旋转至BD,且
 ,直线DO交直线y=x+3
,直线DO交直线y=x+3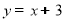 于P点,求P点坐标.
于P点,求P点坐标.
相关试题

