【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,请写出m的取值范围.
参考答案:
【答案】
(1)证明:△=64m2﹣4m(16m﹣1)
=4m,
∵m>0,
∴△>0,
∴抛物线总与x轴有两个不同的交点
(2)解:根据题意,x1、x2为方程mx2﹣8mx+16m﹣1=0的两根,
∴x1+x2=﹣ ![]() =8,x1x2=
=8,x1x2= ![]() ,
,
∵|x1﹣x2|=2,
∴(x1+x2)2﹣4x1x2=4,
∴82﹣4 ![]() =4,
=4,
∴m=1,
∴抛物线的解析式为y=x2﹣8x+15
(3)解:抛物线的对称轴为直线x=﹣ ![]() =4,
=4,
∵抛物线开口向上,
∴当x=2,y≥0时,抛物线与线段CD有交点,
∴4m﹣16m+16m﹣1≥0,
∴m≥ ![]()
【解析】(1)证明△>0即可;(2)利用抛物线与x轴的交点问题,则x1、x2为方程mx2﹣8mx+16m﹣1=0的两根,利用根与系数的关系得到x1+x2=8,x1x2= ![]() ,再变形|x1﹣x2|=2得到(x1+x2)2﹣4x1x2=4,所以82﹣4
,再变形|x1﹣x2|=2得到(x1+x2)2﹣4x1x2=4,所以82﹣4 ![]() =4,然后解出m即可得到抛物线解析式;(3)先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m﹣16m+16m﹣1≥0,然后解不等式即可.
=4,然后解出m即可得到抛物线解析式;(3)先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m﹣16m+16m﹣1≥0,然后解不等式即可.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列要求,解答相关问题.
请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某县政府为了迎接“八一”建军节,加强军民共建活动,计划从花园里拿出1430盆甲种花卉和1220盆乙种花卉,搭配成A、B两种园艺造型共20个,在城区内摆放,以增加节日气氛,已知搭配A、B两种园艺造型各需甲、乙两种花卉数如表所示:(单位:盆)
(1)某校某年级一班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮忙设计出来.
(2)如果搭配及摆放一个A造型需要的人力是8人次,搭配及摆放一个B造型需要的人力是11人次,哪种方案使用人力的总人次数最少,请说明理由.
造型数量花
A
B
甲种
80
50
乙种
40
90
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=


求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发
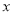 (h)时,汽车与甲地的距离为
(h)时,汽车与甲地的距离为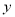 (km),
(km),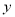 与
与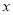 的函数关系如图所示.
的函数关系如图所示.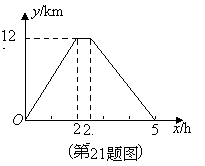
根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中
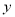 与
与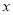 之间的函数表达式;
之间的函数表达式;(3)求这辆汽车从甲地出发4h时与甲地的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与x轴,y轴分别交于点A、B,与函数
的图象与x轴,y轴分别交于点A、B,与函数 的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数 和
和 的图象于点C、D.
的图象于点C、D.(1)求点M、点A的坐标;
(2)若OB=CD,求a的值,并求此时四边形OPCM的面积.

相关试题

