【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=![]()

求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
参考答案:
【答案】(1)![]() ;(2)△ABC为直角三角形
;(2)△ABC为直角三角形
【解析】试题分析:(1)由CD垂直于AB,得到三角形BCD与三角形ACD都为直角三角形,由BC与DB,利用勾股定理求出CD的长,再利用勾股定理求出AD的长即可;
(2)三角形ABC为直角三角形,理由为:由BD+AD求出AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形.
解:(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,BC=3,DB=,
根据勾股定理得:CD=![]() =
=![]() ,
,
在Rt△ACD中,AC=4,CD=![]() ,
,
根据勾股定理得:AD=![]() =
=![]() ;
;
(2)△ABC为直角三角形,理由为:
∵AB=BD+AD=+![]() =5,
=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个三角形中,若一条边等于另一条边的两倍,则称这种三角形为“倍边三角形”. 例如:边长为a=2,b=3,c=4的三角形就是一个倍边三角形.
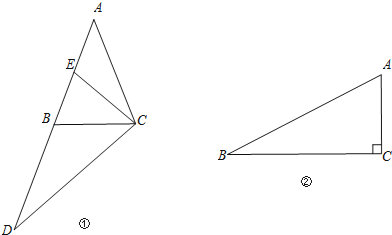
(1)如果一个倍边三角形的两边长为6和8,那么第三条边长所有可能的值为 .
(2)如图①,在△ABC中,AB=AC,延长AB到D,使BD=AB,E是AB的中点.
求证:△DCE是倍边三角形;
(3)如图②,Rt△ABC中,∠C=90°,AC=4,BC=8,若点D在边AB上(点D不与A、B重合),且△BCD是倍边三角形,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.

(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣4,2),C(﹣3,4).
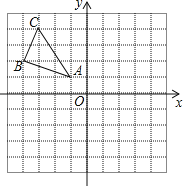
(1)请画出△ABC向右平移5个单位长度后得到△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①(﹣2x)(4x2﹣2x+1) ②(6a3﹣4a2+2a)÷2a
③a4 +(a2)4 -(a2)2 ④

⑤(2a+b)2 ⑥ (3x+7y)(3x-7y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A. 等边三角形 B. 平行四边形 C. 矩形 D. 圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x﹣x3=______.
相关试题

