【题目】(本题满分8分)
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发![]() (h)时,汽车与甲地的距离为
(h)时,汽车与甲地的距离为![]() (km),
(km),![]() 与
与![]() 的函数关系如图所示.
的函数关系如图所示.
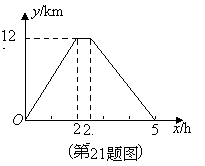
根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
参考答案:
【答案】
(1)不同,理由略。
(2)![]()
(3)48km
【解析】(本题满分8分)
解:(1)不同.理由如下:
![]() 往、返距离相等,去时用了2小时,而返回时用了2.5小时,
往、返距离相等,去时用了2小时,而返回时用了2.5小时,
![]() 往、返速度不同.···············································(2分)
往、返速度不同.···············································(2分)
(2)设返程中![]() 与
与![]() 之间的表达式为
之间的表达式为![]() ,
,
则![]()
解之,得![]() ·····················································(5分)
·····················································(5分)
![]()
![]() .(
.(![]() )(评卷时,自变量的取值范围不作要求)·························(6分)
)(评卷时,自变量的取值范围不作要求)·························(6分)
(3)当![]() 时,汽车在返程中,
时,汽车在返程中,
![]() .
.
![]() 这辆汽车从甲地出发4h时与甲地的距离为48km.·····························(8分)
这辆汽车从甲地出发4h时与甲地的距离为48km.·····························(8分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=


求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,请写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 的图象与x轴,y轴分别交于点A、B,与函数
的图象与x轴,y轴分别交于点A、B,与函数 的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数 和
和 的图象于点C、D.
的图象于点C、D.(1)求点M、点A的坐标;
(2)若OB=CD,求a的值,并求此时四边形OPCM的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
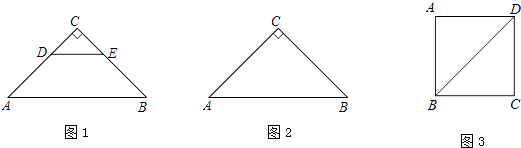
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为 ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.

(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
 纸盒
纸盒
纸板竖式纸盒(个)
横式纸盒(个)
x
正方形纸板(张)
2(100-x)
长方形纸板(张)
4x
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板
 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100< <110,则
<110,则 的值是 .
的值是 .
相关试题

