【题目】如图,长方形![]() 的各边分别平行于
的各边分别平行于![]() 轴或
轴或![]() 轴,物体甲和物体乙分别由点
轴,物体甲和物体乙分别由点![]() 同时出发,沿长方形
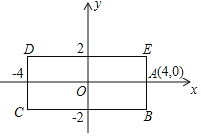
同时出发,沿长方形![]() 的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是____.
参考答案:
【答案】![]()
【解析】
利用行程问题中的相遇问题,由于矩形的边长为8和4,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
矩形的边长为8和4,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为24×1,物体甲行的路程为24×![]() =8物体乙行的路程为24×
=8物体乙行的路程为24×![]() =16,在BC边相遇;
=16,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为24×2,物体甲行的路程为24×2×![]() =16,物体乙行的路程为24×2×
=16,物体乙行的路程为24×2×![]() =32,在DE边相遇;
=32,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为24×3,物体甲行的路程为24×3×![]() =24,物体乙行的路程为24×3×
=24,物体乙行的路程为24×3×![]() =48,在A点相遇;
=48,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2020÷3=673…1,
故两个物体运动后的第2019次相遇地点的是点A,
即物体甲行的路程为24×1×![]() =8,物体乙行的路程为24×1×
=8,物体乙行的路程为24×1×![]() =16时,达到第2020次相遇,
=16时,达到第2020次相遇,
此时相遇点的坐标为:(-2,2),
故答案为:(-2,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y1=
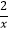 (x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=
(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2= 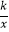 (k<0,x<0)的图象于点B.
(k<0,x<0)的图象于点B.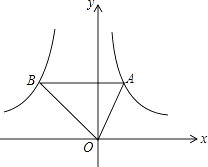
(1)若S△AOB的面积等于3,则k是=;
(2)当k=﹣8时,若点A的横坐标是1,求∠AOB的度数;
(3)若不论点A在何处,反比例函数y2=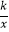 (k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
(k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题:
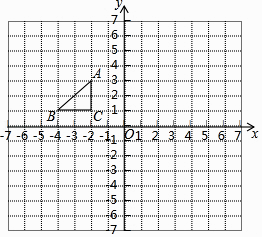
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
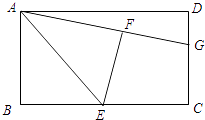
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意三角形ABC,
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.

相关试题

