【题目】已知任意三角形ABC,
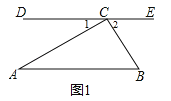
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

参考答案:
【答案】(1)证明见解析(2)三角形的内角和为180°(3)∠AGF=∠AEF+∠F(4)29.5
【解析】试题分析:(1)根据平行线的性即可得到结论;
(2)因为平角为180°,若能运用平行线的性质,将三角形三个内角集中到同一顶点,并得到一个平角,问题即可解决;
(3)根据平角的定义和三角形的内角和定理即可得到结论;
(4)根据平行线的性质得到∠DEB=119°,∠AED=61°,由角平分线的性质得到∠DEF=59.5°,根据三角形的外角的性质即可得到结论.
试题解析:证明:(1)∵DE∥BC,∴∠DCA=∠A;
(2)如图1所示,在△ABC中,∵DE∥BC,∴∠B=∠1,∠C=∠2(内错角相等).
∵∠1+∠BAC+∠2=180°,∴∠A+∠B+∠C=180°.
即三角形的内角和为180°;
(3)∵∠AGF+∠FGE=180°,由(2)知,∠GEF+∠EG+∠FGE=180°,∴∠AGF=∠AEF+∠F;
(4)∵AB∥CD,∠CDE=119°,∴∠DEB=119°,∠AED=61°,∵GF交∠DEB的平分线EF于点F,∴∠DEF=59.5°,∴∠AEF=120.5°,∵∠AGF=150°,∵∠AGF=∠AEF+∠F,∴∠F=150°﹣120.5°=29.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
 .四个结论中正确结论的概率是( )
.四个结论中正确结论的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
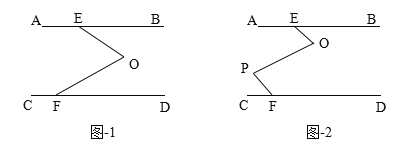
查看答案和解析>>【题目】如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)说明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图-2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a(2a﹣1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2+4x﹣5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着市场竞争日益激烈,某商品一个月内连续两次降价,第一次降价10%,第二次再降价10%后,售价为810元,则原售价为( )
A.900元B.1000元C.960元D.920元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队在一次联赛中共进行了10场比赛,已知10场比赛的平均得分为88分,且前9场比赛的得分依次为:97、91、85、91、84、86、85、82、88.
(1)求第10场比赛的得分;
(2)求这10场比赛得分的中位数,众数和方差.
相关试题

