【题目】阅读下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如:![]() ;
;![]() 等。那么如何求出它们的解集呢?
等。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负,其字母表达式为:
(1)若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]() .
.
请解答下列问题:
(1)反之:①若![]() 则
则![]() 或
或![]() ;②若
;②若![]() ,则__________;
,则__________;
(2)根据上述规律,求不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)②![]() 或
或![]() ;(2)x>2或x<-1.
;(2)x>2或x<-1.
【解析】
(1)根据“异号两数相除,得负”进行分析解答即可;
(2)根据“同号两数相除,得正”,把分式不等式![]() 转化为不等式组:
转化为不等式组:![]() 或
或![]() ,解不等式组即可得到原分式不等式的解集.
,解不等式组即可得到原分式不等式的解集.
(1)②若![]() ,则由“异号两数相除得负”可得:
,则由“异号两数相除得负”可得:![]() 或
或![]() ;
;
(2)∵![]() ,
,
∴![]() 或
或 ![]() ,
,
解得:![]() 或
或![]() ,
,
∴不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
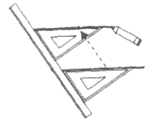
查看答案和解析>>【题目】如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是
 中BC边上的中线,则
中BC边上的中线,则 ,
,理由:
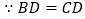 ,
, ,
,即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,
 的面积为a。
的面积为a。(1)如图2,延长
 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若 的面积为
的面积为 ,则
,则 (用含a的代数式表示);
(用含a的代数式表示);(2)如图3,延长
 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若 的面积为
的面积为 ,则
,则 _________(用含a的代数式表示);
_________(用含a的代数式表示);(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到
 (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为 ,则
,则 ________(用含a的代数式表示)
________(用含a的代数式表示)(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.

(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】应用题
有A、B两个商场以同样价格出售同样商品,且各自推出了不同的优惠方案:
在A商场累计购物超过200元后,超出部分按80%收费;
在B商场累计购物满100元后,超出的部分按90%收费。
设累计购物x(x>200)元,用x表示A、B两商场的实际费用并指明顾客选择到哪家购物合适?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个不相等的有理数a,b,我们规定符号
 表示a,b中的较大值,如
表示a,b中的较大值,如 ,
, ,请解答下列问题:
,请解答下列问题:(1)
 _______________;
_______________;(2)如果
 ,求x的取值范围;
,求x的取值范围;(3)如果
 ,求x的值
,求x的值
相关试题

