【题目】油电混合动力汽车是一种节油、环保的新技术汽车,某品牌油电混合动力汽车与普通汽车的相关成本数据估算如下表:
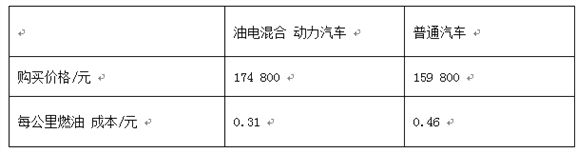
李老师计划购入一辆该品牌的油电混合动力汽车,在只考虑车价和燃油成本的情况下,李老师预估了未来10年的用车成本,发现10年中平均每年行驶总里程达到一定公里数时,选择油电混合动力汽车的成本不高于普通汽车.李老师预估的10年中平均每年行驶的总里程数至少为多少公里?
参考答案:
【答案】至少为10 000公里.
【解析】试题分析:设10年中平均每年行驶的总里程为![]() 公里,然后依据选择油电混合动力汽车的成本不高于普通汽车列不等式求解即可.
公里,然后依据选择油电混合动力汽车的成本不高于普通汽车列不等式求解即可.
试题解析: 设10年中平均每年行驶的总里程为x公里,
根据题意得:![]()
解得:![]()
∴x的最小值为10000.
答:10年中平均每年行驶的总里程数至少为10000公里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
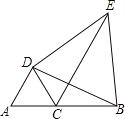
(1)求证:△DAB≌△DCE;
(2)求证:DA∥EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20 t,桃子12 t.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4 t和桃子1 t,一辆乙种货车可装枇杷和桃子各2 t.
(1)王灿如何安排甲、乙两种货车可一次性运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n.
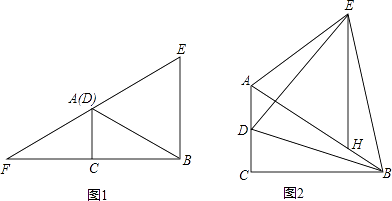
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
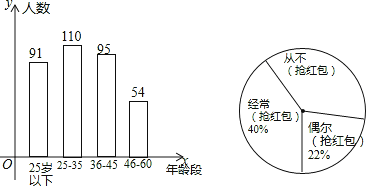
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.

(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.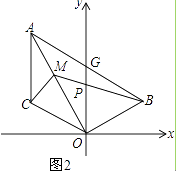
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
相关试题

