【题目】如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
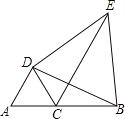
(1)求证:△DAB≌△DCE;
(2)求证:DA∥EC.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)由∠ADC=∠BDE=60°,可得到∠ADB=∠CDE,从而证出
△DAB≌△DCE;(2)由(1)知△DAB≌△DCE推出∠DCE=∠ADC,据同位角相等两直线平行,即可求解.
本题解析:(1)证明:∵△DAC和△DBE都是等边三角形,∴DA=DC,DB=DE,∠ADC=∠BDE=60°,∴∠ADC+∠CDB=∠BDE+∠CDB,即∠ADB=∠CDE,
在△DAB和△DCE中,
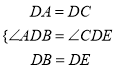 ,
,
∴△DAB≌△DCE(SAS);
(2)∵△DAB≌△DCE,∴∠A=∠DCE=60°,
∵∠ADC=60°,∴∠DCE=∠ADC,
∴DA∥EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角是1440°,求这个多边形的多数是( )
A.7
B.8
C.9
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20 t,桃子12 t.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4 t和桃子1 t,一辆乙种货车可装枇杷和桃子各2 t.
(1)王灿如何安排甲、乙两种货车可一次性运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n.
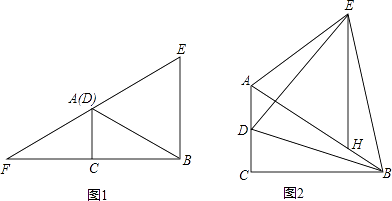
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】油电混合动力汽车是一种节油、环保的新技术汽车,某品牌油电混合动力汽车与普通汽车的相关成本数据估算如下表:
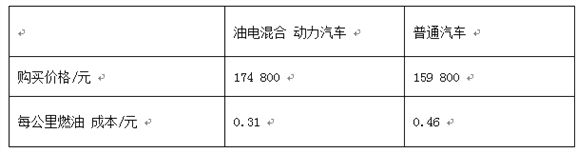
李老师计划购入一辆该品牌的油电混合动力汽车,在只考虑车价和燃油成本的情况下,李老师预估了未来10年的用车成本,发现10年中平均每年行驶总里程达到一定公里数时,选择油电混合动力汽车的成本不高于普通汽车.李老师预估的10年中平均每年行驶的总里程数至少为多少公里?
相关试题

