【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC. 
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标. 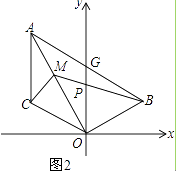
参考答案:
【答案】
(1)解:△AOG的形状是等腰三角形,
理由如下:
∵AC∥y轴,
∴∠CAO=∠GOA,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GOA=∠GAO,
∴AG=OG,
∴△AOG是等腰三角形
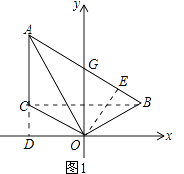
(2)解:如图1,接连BC,过O作OE⊥AB于E,过点C作CD⊥x轴于点D,
∵B、C关于y轴对称,AC∥y轴,
∴AC⊥BC,
在Rt△COD和Rt△BOE中,
![]() ,
,
∴△COD≌△BOE(HL),
∴∠DCO=∠EBO,
∴∠BAC+∠BOC=180°,
设∠BAO=∠CAO=x,∠OBC=∠OCB=y,
∴2x+∠BOC=180°,
又∵2y+∠BOC=180°,
∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,
∴AO⊥OB
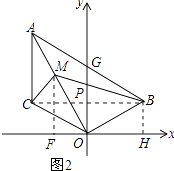
(3)解:如图2,连BC,作MF⊥x轴于F,BH⊥x轴于H,
则∠ACB=90°,
∵∠ACM=45°,
∴CM平分∠ACB,又AM平分∠BAC,
∴BM平分∠ABC,设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z
∴∠OMB=∠OBM,
∴OM=OB
∴△OBM为等腰直角三角形,
∵ 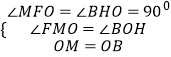 ,
,
∴△OMF≌△OBH(AAS),
∴OF=BH=1,MF=OH=3,
∴M(﹣1,3)
【解析】(1)△AOG的形状是等腰三角形,利用已知条件证明AG=OG即可;(2)接连BC,易证△COD≌△BOE(HL),设∠BAO=∠CAO=x,∠OBC=∠OCB=y,利用全等三角形的性质和已知条件证明∠AOB=∠ACB=90°,即可得到AO⊥BO;(3)连BC,作MF⊥x轴于F,BH⊥x轴于H,易证△OMF≌△OBH,OF=BH=1,MF=OH=3,所以M(﹣1,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n.
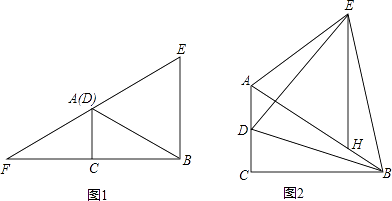
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】油电混合动力汽车是一种节油、环保的新技术汽车,某品牌油电混合动力汽车与普通汽车的相关成本数据估算如下表:
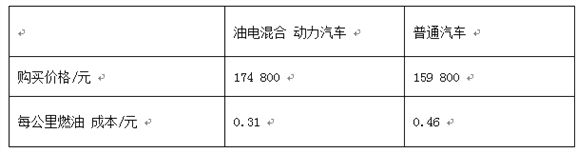
李老师计划购入一辆该品牌的油电混合动力汽车,在只考虑车价和燃油成本的情况下,李老师预估了未来10年的用车成本,发现10年中平均每年行驶总里程达到一定公里数时,选择油电混合动力汽车的成本不高于普通汽车.李老师预估的10年中平均每年行驶的总里程数至少为多少公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
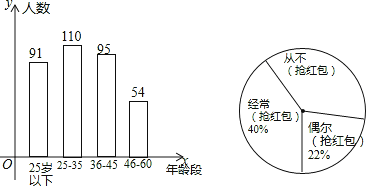
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中正确的是( )
A. (a+b)2=a2+b2B. a2a3=a5C. a8÷a2=a2D. a2+a3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
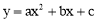 (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.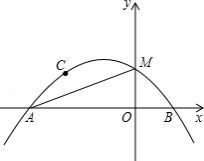
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.
相关试题

