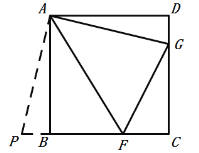
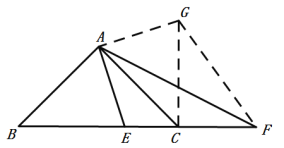
【题目】(1)如图,在正方形 ABCD 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.
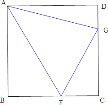
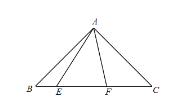
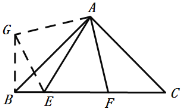
(2)如图,在 Rt△ABC 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,
①写出 BE,CF,EF 之间的数量关系,并证明.
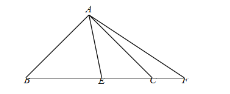
②若将(2)中的△AEF 绕点 A 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则 ![]() = .
= .
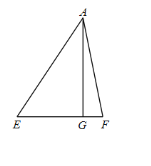
参考答案:
【答案】(1)FG=BF+DG;(2)①EF2=BE2+FC2,理由见解析;②仍然成立;(3)15
【解析】
(1)把△AGD绕点A逆时针旋转90°至△ABP,可使AD与AB重合,再证明△AFG≌△AFP进而得到PF=FG,即可得FG=BF+DG;
(2)①根据△AFC绕点A顺时针旋转90°得到△AGB,根据旋转的性质,可知△ACF≌△ABG得到BG=FC,AG=AF,∠C=∠ABG,∠FAC=∠GAB,根据Rt△ABC中的AB=AC得到∠GBE=90°,所以GB2+BE2=GE2,证△AGE≌△AFE,利用EF=EG得到EF2=BE2+FC2;
②将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点是G,同上的方法证得GC2+CF2=FG2,再设法利用SAS证得△AFG≌△AFE即可求解;
(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,构成正方形ABCD,在Rt△EFC中,利用勾股定理求得正方形的边长,即可求得AG的长,从而求得答案.
(1)∵四边形ABCD为正方形,
∴AB=AD,∠ADC=∠ABC=90°,
∴把△AGD绕点A逆时针旋转90°至△ABP,使AD与AB重合,
∴∠BAP=∠DAG,AP= AG,
∵∠BAD=90°,∠FAG=45°,
∴∠BAF+∠DAG=45°,
∴∠PAF=∠FAG=45°,
∵∠ADC=∠ABC=90°,
∴∠FBP=180°,点F、B、P共线,
在△AFG和△AFP中,
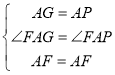 ,
,
∴△AFG≌△AFP(SAS),
∴PF=FG,
即:FG=BF+DG;
(2)①FC2+BE2=EF2,证明如下:
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
将△AFC绕点A顺时针旋转90°得到△AGB,
∴△ACF≌△ABG,
∴BG=FC,AG=AF,∠C=∠ABG=45°,∠FAC=∠GAB,
∴∠GBE=∠ABG +∠ABC =90°,
∴GB2+BE2=GE2,
又∵∠EAF=45°,
∴∠BAE+∠FAC=45°,
∴∠GAB+∠BAE=45°,
即∠GAE=45°,
在△AGE和△AFE中,
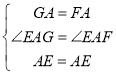 ,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∴FC2+BE2=EF2;
②仍然成立,理由如下:
如图,将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点为点G,
∴△ACG≌△ABE,
∴CG=BE,AG=AE,∠ACG=∠ABE=45°,∠BAE=∠CAG,
∴∠GCB=∠ACB +∠ACG =90°,即∠GCF=90°,
∴GC2+CF2=FG2,
∵∠BAE+∠EAC=∠BAC=90°,
∴∠CAG+∠EAC=90°,
又∵∠EAF=45°,
∴∠GAF=90°-∠EAF=45°,
∴∠GAF=∠EAF=45°,
在△AFG和△AFE中,
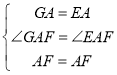 ,
,
∴△AFG≌△AFE(SAS),
∴GF=EF,
∴FC2+BE2=EF2;

(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,
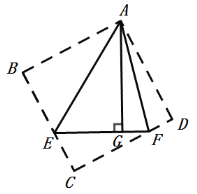
∴△AEG![]() △AEB,△AFG
△AEB,△AFG![]() △AFD,
△AFD,
∴AB=AG=AD,BE=EG=3,DF=FG=2,∠EAG=∠EAB,∠FAG=∠FAD,∠B=∠D=90°,
∵∠EAF=45°,
∴∠EAB+∠FAD=∠EAG+∠FAG=∠EAF=45°,
∴∠BAD=90°,
∴四边形ABCD为正方形,
设AG =![]() ,则AB=BC=CD=
,则AB=BC=CD=![]() ,
,
在Rt△EFC中,EF=3+2=5,EC=BC-BE=![]() ,FC=CD-DF=
,FC=CD-DF=![]() ,
,
∴![]() ,
,
故![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴AG=6,
∴![]() .
.
故答案为:15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在六边形
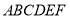 中,
中,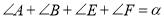 ,
,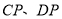 分别平分
分别平分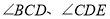 ,则
,则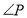 的度数为( )
的度数为( )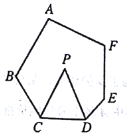
A.
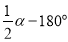 B.
B.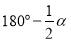 C.
C.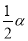 D.
D.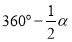
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点A、B的坐标分别为A(a,0),B(b,0),a,b满足方程组
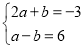 ,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.
,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.(1)求A、B、C三点的坐标;
(2)坐标系中是否存在点P(m,m),使S△PAB=
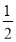 S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.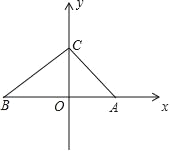
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.
 B.
B.  C.
C. 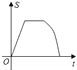 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2,对角线相交于点O.以AB、AO为邻边画平行四边形AOC1B,对角线相交于点O ;以AB、AO 为邻边画平行四边形AO1C2B,对角线相交于点O2 :……以此类推,则平行四边形AO4C5B的面积为( )

A.
 cm2B.
cm2B. cm2C.
cm2C. cm2D.
cm2D.  cm2
cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
相关试题

