【题目】如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.

(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
参考答案:
【答案】(1)10°;(2)13.
【解析】
(1)已知EF垂直平分AC,根据线段垂直平分线的性质定理可得AE=EC,即可得∠EAF=∠C=40°, 再由三角形外角的性质可得∠AED=∠EAF+∠C=80°;已知AD⊥BC,BD=DE, 根据线段垂直平分线的性质定理可得AB=AE,所以∠B=∠AED=80°,由此即可求得∠BAE=20°;又因为AB=AE,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD =![]() ∠BAE=10°;(2)由(1)得,AE=EC=AB,BD=DE,再由△ABC的周长=AB+AC+BC=AB+BD+CD+AC=EC+DE+CD+AC=CD+CD+AC即可求得△ABC的周长.
∠BAE=10°;(2)由(1)得,AE=EC=AB,BD=DE,再由△ABC的周长=AB+AC+BC=AB+BD+CD+AC=EC+DE+CD+AC=CD+CD+AC即可求得△ABC的周长.
(1)∵EF垂直平分AC,
∴AE=EC,
∴∠EAF=∠C=40°,
∴∠AED=∠EAF+∠C=80°;
∵AD⊥BC,BD=DE,
∴AB=AE,
∴∠B=∠AED=80°,
∴∠BAE=20°,
∵AB=AE,AD⊥BC,
∴∠BAD =![]() ∠BAE=10°;
∠BAE=10°;
(2)由(1)得,AE=EC=AB,BD=DE,
∴△ABC的周长=AB+AC+BC=AB+BD+CD+AC=EC+DE+CD+AC=CD+CD+AC=4+4+5=13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )

A. 24° B. 33° C. 42° D. 43°
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的例题:
解方程

解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.
(1)求证:CE=CF;
(2)若等边三角形AEF的边长为2,求正方形ABCD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
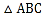 中,
中,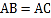 ,D在边AC上,且
,D在边AC上,且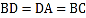 .
.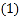 如图1,填空
如图1,填空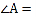 ______
______ ,
,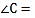 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线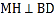 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
 ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=
 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

相关试题

