【题目】如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.
(1)求证:CE=CF;
(2)若等边三角形AEF的边长为2,求正方形ABCD的周长.
参考答案:
【答案】(1)证明见解析(2)2(![]() )
)
【解析】
(1)证明:∵四边形ABCD是正方形,∴AB=AD。
∵△AEF是等边三角形,∴AE=AF。
在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL)。
∴CE=CF。
(2)解:连接AC,交EF于G点,
∵△AEF是等边三角形,△ECF是等腰直角三角形,∴AC⊥EF。
在Rt△AGE中,EG=sin30°AE=![]() ×2=1,∴EC=
×2=1,∴EC=![]() 。
。
设BE=x,则AB=BC=x+![]() ,
,
在Rt△ABE中,AB2+BE2=AE2,即(x+![]() )2+x2=4,解得x=
)2+x2=4,解得x=![]() (负值舍去)。
(负值舍去)。
∴AB=![]() 。
。
∴正方形ABCD的周长为4AB=2(![]() )。
)。
(1)根据正方形可知AB=AD,由等边三角形可知AE=AF,于是可以证明出△ABE≌△ADF,即可得出CE=CF。
(2)连接AC,交EF与G点,由△AEF是等边三角形,△ECF是等腰直角三角形,于是可知AC⊥EF,求出EG=1,设BE=x,利用勾股定理求出x,即可求出AB的值,从而求出正方形的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,在边长为
,在边长为 的小正方形组成的网格中,
的小正方形组成的网格中, 的顶点
的顶点 、
、 均在格点上,点
均在格点上,点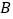 在
在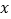 轴上,点
轴上,点 的坐标为
的坐标为 .
.
 点
点 关于点
关于点 中心对称的点的坐标为________;
中心对称的点的坐标为________; 绕点
绕点 顺时针旋转
顺时针旋转 后得到
后得到 ,那么点
,那么点 的坐标为________;线段
的坐标为________;线段 在旋转过程中所扫过的面积是________.
在旋转过程中所扫过的面积是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )

A. 24° B. 33° C. 42° D. 43°
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的例题:
解方程

解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.

(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
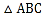 中,
中,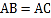 ,D在边AC上,且
,D在边AC上,且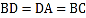 .
.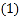 如图1,填空
如图1,填空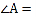 ______
______ ,
,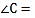 ______
______
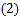 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线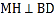 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
 ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=
 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.
相关试题

