【题目】如图,在△ABC中,∠ACB=![]() ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=![]() 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
试题(1)根据三角形的中位线定理可得EF∥BC,根据两组对边分别平行的四边形是平行四边形即可判定四边形ECBF是平行四边形;(2)根据直角三角形中30°的锐角所对的直角边等于斜边的一半和斜边的中线等于斜边的一半可得![]() ,
,![]() ,即可得
,即可得![]() ,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
试题解析: (1) 证明:∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)证法一:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,
,![]() .
.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法二:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,∠ABC=
,∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法三:
∵E为AB的中点,∠ACB=![]() ,∠A=
,∠A=![]() ,
,
∴![]() , ∠ABC=
, ∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD上.
(1)求证:CE=CF;
(2)若等边三角形AEF的边长为2,求正方形ABCD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.

(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,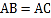 ,D在边AC上,且
,D在边AC上,且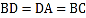 .
.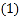 如图1,填空
如图1,填空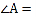 ______
______ ,
,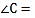 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线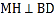 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 如果一件事不可能发生,那么它是必然事件,即发生的概率是

B. 不太可能发生的事情的概率不为

C. 若一件事情肯定发生,则其发生的概率

D. 概率很大的事情必然发生
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人设摊“摸彩”,只见他手持一袋,内装大小、质量完全相同的
 个红球、
个红球、 个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得
个白球,每次让顾客“免费”从袋中摸出两球,如果两球的颜色相同,顾客得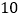 元钱,否则顾客付给这人
元钱,否则顾客付给这人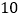 元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
元钱,请你判断一下该活动对顾客________(填“合算”或“不合算”).
相关试题

