【题目】如图,把一个菱形绕着它的对角线的交点旋转![]() ,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为
,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为![]() ,边长为
,边长为![]() ,则该“星形”的面积是__________.
,则该“星形”的面积是__________.

参考答案:
【答案】![]()
【解析】解:在图中标上字母,令AB与A′D′的交点为点E,过E作EF⊥AC于点F,如图所示.

∵四边形ABCD为菱形,AB=2,∠BAD=60°,∴∠BAO=30°,∠AOB=90°,∴AO=ABcos∠BAO=![]() ,BO=ABsin∠BAO=1.
,BO=ABsin∠BAO=1.
同理可知:A′O=![]() ,D′O=1,∴AD′=AO﹣D′O=
,D′O=1,∴AD′=AO﹣D′O=![]() ﹣1.∵∠A′D′O=90°﹣30°=60°,∠BAO=30°,∴∠AED′=30°=∠EAD′,∴D′E=AD′=
﹣1.∵∠A′D′O=90°﹣30°=60°,∠BAO=30°,∴∠AED′=30°=∠EAD′,∴D′E=AD′=![]() ﹣1.
﹣1.
在Rt△ED′F中,ED′=![]() ﹣1,∠ED′F=60°,∴EF=ED′sin∠ED′F=
﹣1,∠ED′F=60°,∴EF=ED′sin∠ED′F=![]() ,∴S阴影=S菱形ABCD+4S△AD′E=
,∴S阴影=S菱形ABCD+4S△AD′E=![]() ×2AO×2BO+4×
×2AO×2BO+4×![]() AD′EF=
AD′EF=![]() .故答案为:
.故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与 轴交于
轴交于 ,
,  两点,与
两点,与 轴交于点
轴交于点 .
.(
 )求抛物线的解析式.
)求抛物线的解析式.(
 )设抛物线的顶点为
)设抛物线的顶点为 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且 ,求点
,求点 的坐标.
的坐标.(
 )点
)点 在直线
在直线 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点 使
使 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点 坐标.
坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四种沿
 折叠的方法中,不一定能判定纸带两条边线
折叠的方法中,不一定能判定纸带两条边线 ,
,  互相平行的是( ).
互相平行的是( ).
A. 如图
 ,展开后测得
,展开后测得
B. 如图
 ,展开后测得
,展开后测得
C. 如图
 ,测得
,测得
D. 如图
 ,展开后再沿
,展开后再沿 折叠,两条折痕的交点为
折叠,两条折痕的交点为 ,测得
,测得 ,
, 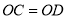
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察思考:如图,
 、
、 是直线
是直线 上的两个定点,点
上的两个定点,点 、
、 在直线
在直线 上运动(点
上运动(点 在点
在点 的左侧),
的左侧), ,已知
,已知 ,
,  、
、 间的距离为
间的距离为 ,连接
,连接 、
、 、
、 ,把
,把 沿
沿 折叠得
折叠得 .
.(
 )当
)当 、
、 两点重合时,则
两点重合时,则 __________
__________  .
.(
 )当
)当 、
、 两点不重合时,
两点不重合时,①连接
 ,探究
,探究 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.②若以
 、
、 、
、 、
、 为顶点的四边形是矩形,画出示意图并直接写出
为顶点的四边形是矩形,画出示意图并直接写出 的长.
的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解九年级学生的体能情况,随机抽取部分男生进行引体向上测试,并根据抽测成绩绘制成如下两幅统计图.


(
 )本次抽测的学生总人数为__________;请你补全图
)本次抽测的学生总人数为__________;请你补全图 的统计图.
的统计图.(
 )本次抽测成绩的众数为__________次;中位数为__________次.
)本次抽测成绩的众数为__________次;中位数为__________次.(
 )若规定引体向上
)若规定引体向上 次以上(含
次以上(含 次)为体能达到优秀,则该校
次)为体能达到优秀,则该校 名九年级男生中,估计有多少人能达到优秀?
名九年级男生中,估计有多少人能达到优秀? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
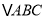 中,
中, 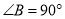 ,以
,以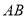 上的一点
上的一点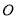 为圆心,以
为圆心,以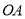 为半径的圆交
为半径的圆交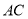 于点
于点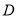 ,交
,交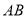 于点
于点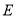 .
.
(
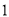 )求证:
)求证: 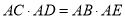 .
.(
 )如果
)如果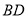 是⊙
是⊙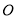 的切线,
的切线, 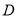 是切点,
是切点, 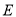 是
是 的中点,当
的中点,当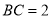 时,求
时,求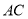 的长.
的长.
相关试题

