Question

【题目】在平面直角坐标系中，抛物线与轴交于， 两点，与轴交于点．

（）求抛物线的解析式．

（）设抛物线的顶点为，点在抛物线的对称轴上，且，求点的坐标．

（）点在直线上方的抛物线上，是否存在点使的面积最大，若存在，请求出点坐标．

Answer 1

【答案】（）（） 或（）存在， ．

【解析】试题分析：（1）将A、B的坐标代入抛物线的解析式中，即可求出待定系数的值；

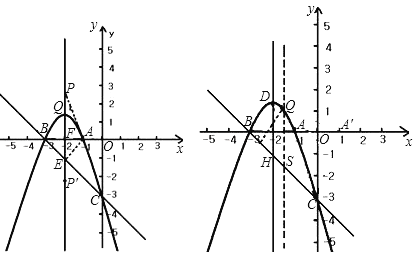
（2）根据（1）得到的函数解析式，可求出D、C的坐标；易证得△OBC是等腰Rt△，若过A作BC的垂线，设垂足为E，在Rt△ABE中，根据∠ABE的度数及AB的长即可求出AE、BE、CE的长；连接AC，设抛物线的对称轴与x轴的交点为F，若∠APD=∠ACB，那么△AEC与△AFP，根据得到的比例线段，即可求出PF的长，也就求得了P点的坐标；

（3）当Q到直线BC的距离最远时，△QBC的面积最大（因为BC是定长），可过Q作y轴的平行线，交BC于S；根据B、C的坐标，易求出直线BC的解析式，可设出Q点的坐标，根据抛物线和直线BC的解析式，分别表示出Q、S的纵坐标，即可得到关于QS的长以及Q点横坐标的函数关系式，以QS为底，B、C横坐标差的绝对值为高可得到△QBC的面积，由于B、C横坐标差的绝对值为定值，那么QS最长时，△QBC的面积最大，此时Q离BC的距离最远；可根据上面得到的函数的性质求出QS的最大值及对应的Q点横坐标，然后将其代入抛物线的解析式中，即可求出Q点的坐标．

试题解析：解：（1）∵抛物线y=﹣x2+bx+c经过A（﹣1，0），B（﹣3，0），∴，

解得： ，∴抛物线的解析式为y=﹣x2﹣4x﹣3；

（2）由y=﹣x2﹣4x﹣3，可得D（﹣2，1），C（0，﹣3），∴OB=3，OC=3，OA=1，AB=2，可得△OBC是等腰直角三角形，∴∠OBC=45°，CB=，如图，设抛物线对称轴与x轴交于点F，∴AF=AB=1，过点A作AE⊥BC于点E，∴∠AEB=90°，可得BE=AE= ，CE=，在△AEC与△AFP中，∠AEC=∠AFP=90°，∠ACE=∠APF，∴△AEC∽△AFP，∴， ，解得PF=2，∵点P在抛物线的对称轴上，∴点P的坐标为（﹣2，2）或（﹣2，﹣2）；

（3）存在，因为BC为定值，当点Q到直线BC的距离最远时，△BCQ的面积最大，设直线BC的解析式y=kx+b，直线BC经过B（﹣3，0），C（0，﹣3），∴，

解得：k=﹣1，b=﹣3，∴直线BC的解析式y=﹣x﹣3，设点Q（m，n），过点Q作QH⊥BC于H，并过点Q作QS∥y轴交直线BC于点S，则S点坐标为（m，﹣m﹣3），∴QS=n﹣（﹣m﹣3）=n+m+3，∵点Q（m，n）在抛物线y=﹣x2﹣4x﹣3上，∴n=﹣m2﹣4m﹣3，∴QS=﹣m2﹣4m﹣3+m+3=﹣m2﹣3m=﹣（m+）2+，当m=﹣时，QS有最大值，∵BO=OC，∠BOC=90°，∴∠OCB=45°．

∵QS∥y轴，∴∠QSH=45°，∴△QHS是等腰直角三角形，∴当斜边QS最大时QH最大，∵当m=﹣时，QS最大，∴此时n=﹣m2﹣4m﹣3=﹣+6﹣3=，∴Q（﹣， ），∴Q点的坐标为（﹣， ）时，△BCQ的面积最大．