Question

【题目】如图，在正方形OABC中，点B的坐标是（4，4），点E、F分别在边BC、BA上，OE=2，若∠EOF＝45°，则F点的纵坐标是（ ）

A. B. 1 C. D. -1

Answer 1

【答案】A

【解析】分析：如图连接EF，延长BA使得AM=CE，则△OCE≌△OAM．再证明△OFE≌△FOM，根据全等三角形的性质和图形即可得EF=FM=AF+AM=AF+CE，根据勾股定理求得OE的长，设AF=x，则EF=2+x，EB=2，FB=4-x，在Rt△BEF中，根据勾股定理可得方程（2+x）2=22+（4-x）2，解方程求得x值，即可得点F的纵坐标.

详解：如图连接EF，延长BA使得AM=CE，则△OCE≌△OAM．

∴OE=OM，∠COE=∠MOA，

∵∠EOF=45°，

∴∠COE+∠AOF=45°，

∴∠MOA+∠AOF=45°，

∴∠EOF=∠MOF，

在△OFE和△OFM中，

，

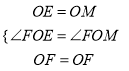∴△OFE≌△FOM，

∴EF=FM=AF+AM=AF+CE，设AF=x，

∵CE=，

∴EF=2+x，EB=2，FB=4-x，

∴（2+x）2=22+（4-x）2，

∴x=，

∴点F的纵坐标为，

故选A．