【题目】抛物线y=ax2+bx﹣4与x轴交于A,B两点,(点B在点A的右侧)且A,B两点的坐标分别为(﹣2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:将A(﹣2,0),B(8,0)代入抛物线y=ax2+bx﹣4得:
![]() ,
,
解得: 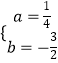 ,
,
∴抛物线的解析式:y= ![]() x2﹣
x2﹣ ![]() x﹣4
x﹣4
(2)
解:当x=0时,y=﹣4,
∴C(0,﹣4),
∴OC=4,
∵四边形DECB是菱形,
∴OD=OC=4,
∴D(0,4),
设BD的解析式为:y=kx+b,
把B(8,0)、D(0,4)代入得: ![]() ,
,
解得: 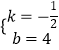 ,
,
∴BD的解析式为:y=﹣ ![]() x+4,
x+4,
∵l⊥x轴,
∴M(m,﹣ ![]() m+4)、Q(m,
m+4)、Q(m, ![]() m2﹣
m2﹣ ![]() m﹣4),
m﹣4),
如图1,∵MQ∥CD,
∴当MQ=DC时,四边形CQMD是平行四边形,
∴(﹣ ![]() m+4)﹣(
m+4)﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)=4﹣(﹣4),
m﹣4)=4﹣(﹣4),
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4,
∴当m=4时,四边形CQMD是平行四边形

(3)
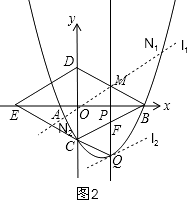
解:如图2,要使三角形BCN的面积等于三角形BCQ的面积,N点到BC的距离与Q到BC的距离相等;
设直线BC的解析式为:y=kx+b,
把B(8,0)、C(0,﹣4)代入得: ![]() ,
,
解得: 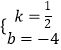 ,
,
∴直线BC的解析式为:y= ![]() x﹣4,
x﹣4,
由(2)知:当P(4,0)时,四边形DCQM为平行四边形,
∴BM∥QC,BM=QC,
得△MFB≌△QFC,
分别过M、Q作BC的平行线l1、l2,
所以过M或Q点的斜率为的 ![]() 直线与抛物线的交点即为所求,
直线与抛物线的交点即为所求,
当m=4时,y=﹣ ![]() m+4=﹣
m+4=﹣ ![]() ×4+4=2,
×4+4=2,
∴M(4,2),
当m=4时,y= ![]() m2﹣
m2﹣ ![]() m﹣4=
m﹣4= ![]() ×16﹣
×16﹣ ![]() ×4﹣4=﹣6,
×4﹣4=﹣6,
Q(4,﹣6),
①设直线l1的解析式为:y= ![]() x+b,
x+b,
∵直线l1过Q点时,
∴﹣6= ![]() ×4+b,b=﹣8,
×4+b,b=﹣8,
∴直线l1的解析式为:y= ![]() x﹣8,
x﹣8,
则 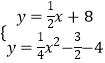 ,
,
![]() =
= ![]() x﹣8,
x﹣8,
解得x1=x2=4(与Q重合,舍去),
②∵直线l2过M点,
同理求得直线l2的解析式为:y= ![]() x,
x,
则 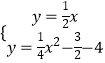 ,
,
![]() =
= ![]() x,
x,
x2﹣x﹣16=0,
解得x1=4+4 ![]() ,x2=4﹣4
,x2=4﹣4 ![]() ,
,
代入y= ![]() x,得
x,得 ![]() ,
, ![]() ,
,
则N1(4+4 ![]() ,2+2
,2+2 ![]() ),N2(4﹣4
),N2(4﹣4 ![]() ,2﹣2
,2﹣2 ![]() ),
),
故符合条件的N的坐标为N1(4+4 ![]() ,2+2
,2+2 ![]() ),N2(4﹣4
),N2(4﹣4 ![]() ,2﹣2
,2﹣2 ![]() ).
).
【解析】(1)直接将A、B两点的坐标代入抛物线的解析式中,列方程组可求a、b的值,写出解析式即可;(2)先求点C和D的坐标,求直线BD的解析式,根据横坐标m表示出点Q和M的纵坐标,由MQ∥CD,根据一组对边平行且相等的四边形是平行四边形,证明MQ=CD即可,因此列等式:(﹣ ![]() m+4)﹣(
m+4)﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)=4﹣(﹣4),求m即可;(3)要使三角形BCN的面积等于三角形BCQ的面积,可先判断四边形CQBM是平行四边形,解得M点到BC的距离与Q到BC的距离相等,所以过M或Q点的与直线BC平行的直线与抛物线的交点即为所求,列方程组可得结论.
m﹣4)=4﹣(﹣4),求m即可;(3)要使三角形BCN的面积等于三角形BCQ的面积,可先判断四边形CQBM是平行四边形,解得M点到BC的距离与Q到BC的距离相等,所以过M或Q点的与直线BC平行的直线与抛物线的交点即为所求,列方程组可得结论.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.

(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第(100)个图案有___________________个三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2
 ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )
A.
 B. 1 C.
B. 1 C.  D.
D.  -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=
 ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )

A.
B.
C.
D.
相关试题

