【题目】已知函数![]() 与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.
与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.

(1)直接写出A、B两点的坐标:A(______,_____)、B(_____,_____);
(2)在AB上找一点P,当PC+PO最小时,在AC上找一点Q使得PQ+![]() 最小,求Q点坐标;
最小,求Q点坐标;
(3)在(2)的条件下,平面内能否找到一点K,使得点A、C、P、K构成的四边形是平行四边形,若能,直接写出K点坐标,若不能,请说明理由.
参考答案:
【答案】(1)(![]() ,0),(0,6);(2)Q(
,0),(0,6);(2)Q(![]() );(3)能,K(
);(3)能,K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).
【解析】
(1)在一次函数解析式中,分别令y=0和x=0即可求出A、B的坐标;
(2)作点O关于AB的对称点O′,连接C O′与AB交于P点,则P点即为使得CP+OP最小的点.过O′作O′D⊥x轴.可求出 O′的坐标,O′C的解析式.由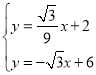 得P的坐标.过Q作QH⊥x轴于H,与AC交于Q点.由含30°直角三角形的性质可得QH=
得P的坐标.过Q作QH⊥x轴于H,与AC交于Q点.由含30°直角三角形的性质可得QH=![]() AQ,即可得到当PH⊥x轴时与AC交点Q即为所求,即可得出点Q的坐标;
AQ,即可得到当PH⊥x轴时与AC交点Q即为所求,即可得出点Q的坐标;
(3)设K(x,y),点A、C、P、K构成的四边形是平行四边形,分三种情况讨论:
①若AK,CP是对角线;②若AP,CK是对角线;③若AC,KP是对角线,;分别利用平行四边形对角线的交点平分对角线和中点坐标公式即可得出点K的坐标.
(1)在![]() 中,令y=0,解得:x=
中,令y=0,解得:x=![]() ,令x=0,解得:y=6,∴A(
,令x=0,解得:y=6,∴A(![]() ,0),B(0,6);
,0),B(0,6);
(2)作点O关于AB的对称点O′,连接C O′与AB交于P点,则P点即为使得CP+OP最小的点.过O′作O′D⊥x轴.
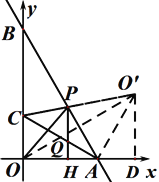
∵OA=![]() ,OB=6,∴AB=
,OB=6,∴AB=![]() ,∴∠ABO=30,∠BAO=60,∴O′A=OA=
,∴∠ABO=30,∠BAO=60,∴O′A=OA=![]() ,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=
,∠O′AB=∠OAB=60 ∴∠O'AD=60°,∴∠AO'D=30°,∴O′D=3,AD=![]() ,∴ O′(
,∴ O′(![]() ,3),易求O′C解析式为:
,3),易求O′C解析式为:![]() .
.
由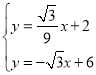 得P(
得P(![]() ,
,![]() ).
).
过Q作QH⊥x轴于H,与AC交于Q点.
∵OC=2,OA=![]() ,∴∠CAO=30,∴QH=
,∴∠CAO=30,∴QH=![]() AQ,∴当PH⊥x轴时与AC交点Q即为所求.
AQ,∴当PH⊥x轴时与AC交点Q即为所求.
易求直线AC的解析式为![]() ,把x=
,把x=![]() 代入
代入![]() ,得y=
,得y=![]() ,∴Q(
,∴Q(![]() ).
).
(3)设K(x,y).
∵P(![]() ,
,![]() ),A(
),A(![]() ,0),C(0,2),点A、C、P、K构成的四边形是平行四边形,∴分三种情况讨论:
,0),C(0,2),点A、C、P、K构成的四边形是平行四边形,∴分三种情况讨论:
①若AK,CP是对角线,则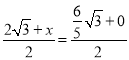 ,
,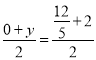 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
②若AP,CK是对角线,则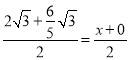 ,
,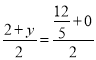 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
③若AC,KP是对角线,则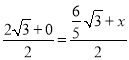 ,
,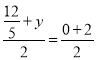 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,∴ K(
,∴ K(![]() ,
,![]() );
);
综上所述:K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() )或K(
)或K(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax2﹣
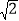 ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB(1)求这条抛物线的解析式及直线BC的解析式;
(2)设点D为抛物线对称轴上的一点,当点D在对称轴上运动时,是否可以与点C,A,B三点,构成梯形的四个顶点?若可以,求出点D坐标,若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
-
科目: 来源: 题型:
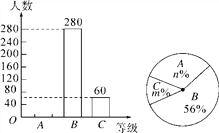
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
-
科目: 来源: 题型:
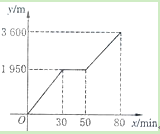
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
相关试题

