【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是

A.①②③④B.①②③C.②④D.①③
参考答案:
【答案】B
【解析】
根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC=∠CAD,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG=∠ACD,根据角平分线定义即可判断③;根据等腰三角形的判定判断④即可.
解:∵BE是中线,
∴AE=CE,
∴S△ABE=S△BCE(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顶点在网格交点的多边形叫做格点多边形,如图,在一个9 X 9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为l个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△AlBlCl;
(2)在网格中画出△ABC绕点A逆时针旋转900后得到的△AB2C2;
(3)在(1)中△ABC向上平移过程中,求边AC所扫过区域的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(
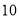 分)如图,管中放置着三根同样的绳子
分)如图,管中放置着三根同样的绳子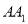 ,
, 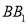 ,
, 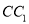 .
.(
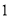 )小明从
)小明从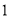 这三根绳子中随机选一根,恰好选中绳子
这三根绳子中随机选一根,恰好选中绳子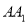 的概率是__________.
的概率是__________.(
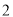 )小明先从左端
)小明先从左端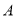 ,
, 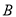 ,
, 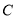 三个绳头中随机选两个打一个结,再从右端
三个绳头中随机选两个打一个结,再从右端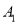 ,
, 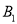 ,
, 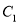 三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(
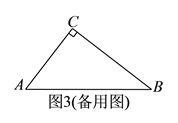
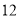 分)如图,在
分)如图,在 中,
中, 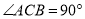 ,
, 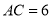 ,
,  ,点
,点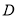 在边
在边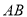 上运动,
上运动, 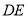 平分
平分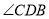 交边
交边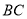 于点
于点 ,
, 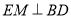 垂足为
垂足为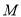 ,
, 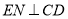 垂足为
垂足为 .
.

(
 )当
)当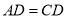 时,求证:
时,求证: 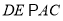 .
.(
 )探究:
)探究: 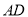 为何值时,
为何值时, 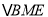 与
与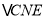 相似?
相似?(
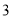 )直接写出:
)直接写出: 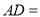 __________时,四边形
__________时,四边形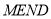 与
与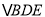 的面积相等.
的面积相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
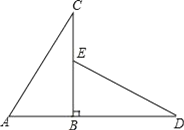
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
-
科目: 来源: 题型:
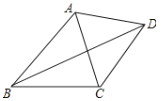
查看答案和解析>>【题目】如图,已知四边形ABCD中,对角线BD平分∠ABC,∠BAC=64°,∠BCD+∠DCA=180°,那么∠BDC为_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,∠ABC与∠ACB的平分线交于点P,根据下列条件,求∠BPC的度数.
(1)若∠A=50°,则∠BPC= ;
(2)从上述计算中,我们能发现:∠BPC= (用∠A表示);
(3)如图2,若BP,CP分别是∠ABC与∠ACB的外角平分线,交于点P,则∠BPC= .(用∠A表示),并说明理由.

相关试题

